结构因果发现
基于图模型的因果结构发现
因果发现的基本假设
马尔可夫等价类(Markov equivalent class):拥有相同d分离结构的因果图并且具有相同条件独立性关系的因果图被称作马尔可夫等价类,无法根据条件独立性分辨因果方向。
因果充分性假设(causal sufficiency assumption):没有未被观测到的混杂变量------该假设为弱假设。
因果马尔可夫假设(causal Markov assumption):所有因果图中的d分离结构均能表明观测数据分布\(P\)中的条件独立性。
因果信念假设(caudal faithfulness assumption):所有观测分布\(P\)中的条件独立性关系均能被因果图中的d分离结构表示。
基于条件独立检验的因果发现(Constraint-based Algorithms)
这一类算法通过找到三种结构来构建因果图,寻找方式就是通过条件独立的检验,一般的方式都是从一个无向的全链接图出发开始寻找,通过一系列规则最终生成一个图。基于条件独立检验的因果发现算法需要满足5.1中的三大基本假设,因此该类方法通常存在以下缺点:
不能存在未观测的混杂变量,该条件在大数据的情况下很难满足,但存在如FCI的算法放宽了该限制。
对于分叉结构以及对撞结构,该类算法无法根据条件独立性分辨马尔可夫等价类,因此对局部因果关系的判别不足。
根据因果信念假设,只能根据条件独立性来判断因果关系,因此需要非常多且高质量的数据,如果数据较少,则条件独立性假设测试可能会互斥。
PC算法
PC 算法仍是将完全图作为初始骨架图, 然后从空集开始逐步增大分离集的大小,不断删除骨架图中的边, 使得每个结点的邻居数不断减少,寻找两个节点的分离集限定在它们的邻居集的子集范围内,目的是避免高维变量的条件独立检验。
依赖关系的确立
设\(V\)是输入点集,有以下步骤:
在V上生成完全无向图 \(G\)
对于\(G\)中两个相邻点\(i,j\),如果\(i\)和\(j\)在给定节点\(k\)时条件独立,则删除\(i\)和\(j\)之间的边
这样会得到一个无向图,图中的无向边表示它连接的两个节点之间有依赖(因果)关系,这样的无向图叫骨架(skeleton)。PC 算法把上述过程转化为了 d 分隔问题。
条件独立性检验算法
用O(i,j)表示能d分隔i和j的点集,用adj(G,x)表示图G中节点x的相邻点集,PC算法具体流程为:

图1 PC算法
依赖(因果)关系方向确立
经过5.2.1.2,我们得到了一个无向图,现在我们要利用d分隔原理来确定图中边的依赖方向,把骨架扩展为\(DAG\)。由于我们已经记录了d分隔\(X\)和\(Y\)的点集\(O\),因此我们可以用d分隔的结论反推出无向图中边的方向,方向判断方法可以转换为以下三条规则:
规则1:如果存在\(X \rightarrow Y - Z\),把\(Y - Z\)变为\(Y \rightarrow Z\)
规则2:如果存在\(X \rightarrow Z \rightarrow Y\),把\(X - Y\)变为\(X \rightarrow Y\)
规则3:如果存在\(X - Z_{1} \rightarrow Y\),\(X - Z_{2} \rightarrow Y\),且\(Z_{1}Z_{2}\)不相邻,把\(X - Y\)变为\(X \rightarrow Y\)

图2 扩展无向图
由此我们可以得到一个完全部分有向无环图(CPDAG),即边集\(E\)中包含有向边和无向边,且\(E\)中的无向边可逆,有向边不可逆。
有向边的可逆与不可逆:对于有向无环图\(G = (V,E)\)中的任意有向边\(V_{i} \rightarrow V_{j} \in E\),如果存在图\(G^{'} = (V,E^{'})\)与\(G\)等价,且\(V_{j} \rightarrow V_{i} \in E^{'}\),则称\(V_{i} \rightarrow V_{j}\)是可逆的,否则不可逆。
无向边的可逆与不可逆:对任意无向边\(V_{i} - V_{j} \in E\),若存在\(G_{1} = (V,E_{1})\)、\(G_{2} = (V,E_{2})\)均与\(G\)等价,且\(V_{i} \rightarrow V_{j} \in E_{1}\)、\(V_{i} \rightarrow V_{j} \in E_{2}\),则称无向边\(V_{i} - V_{j}\)在\(G\)中可逆,否则不可逆。
PC 算法得到的图是含有无向边的。这是因为依据 d 分隔确定的条件独立性所构造的网络结构不具有唯一性,它们只是真实的因果图的马尔科夫等价类。
此外还有许多基于PC算法的变种算法,如FCI算法用以在未观测混杂变量和样本选择偏差存在的情形下学习因果结构, 该方法在 PC 邻接搜索的基础上, 利用额外的条件独立性检验以处理潜在混杂变量。
基于评分模型的因果发现(Scored-based Algorithms)
该类方法是根据评分选择最佳网络. 为每个网络赋一个评分 (如后验概率、BIC(Bayesian information criterion) 和 AIC (Akaike information criterion)等), 搜索最佳评分的有向无环图,常采用贪心法等启发式搜索方法。在整个网络空间搜索最佳评分的网络是一个非常困难的问题.此类方法通过定义可分解的评分准则来评价数据和网络的拟合度,并以该准则指导最优网络结构的搜索。当定义的评分准则满足评分等价性,即等价类中的 DAG (Directed Acylic Graph)拥有相同的分数时,该准则可用于指导因果结构的学习。该类方法仍然存在如下缺点:
无法区分马尔可夫等价类
由于要找到最优分数,就要搜索全部的图,这是一个NP-hard的问题,复杂度极高且容易陷入局部最优。
GES算法
两阶段的贪婪等价搜索算法 (greedy equivalence search, GES)是该类型的一个代表性方法, 它基于观测数据, 从 DAG空间中搜索获取真实分布的完备图,但该方法尚无法处理未观测混杂变量、样本选择偏差等问题。
GES算法建立在Meek预测的理论基础上,因此我们首先简要介绍一下Meek预测的基本内容:如果DAG\(\mathcal{\ H}\)是另一个DAG \(\mathcal{G}\)的独立图(independence map),即\(\mathcal{H}\)结构中隐含的任何独立性均被\(\mathcal{G}\)的结构隐含。那么在\(\mathcal{G}\)中存在一系列有限的边集合可以被添加或者反转方向,并且(1)在每一条可被修改的边被添加或者反转方向后,\(\mathcal{H}\)仍然是\(\mathcal{G}\)的独立图;(2)在所有修改后\(\mathcal{G = H}\)。
在Meek预测为真后,又提出了一个两步贪心算法来使用BIC指标去辨别DAG的等价类,该算法可被总结为以下两步:
从不具有依赖关系的等价类(空图)出发,每次通过考虑所有可能的单条边的添加来贪心地添加依赖关系,从而得到打分函数局部最大的结构图
我们从当前等价类出发,利用贪心原理逐步删除有向边,直到打分函数不再变化,得到最终的因果结构图。
上述GES算法可被一句话总结为:从空图出发,逐步添加当前最需要的边,直到达到打分函数局部最优,然后逐步删除不需要的边,得到最终的因果图。
Meek预测
Meek预测描述了独立图之间的相对关系,如果\(G \leq H\),那么在G中存在一系列有限的边集合可以被添加或者反转方向,并且(1)在每一条可被修改的边被添加或者反转方向后,H仍然是G的独立图;(2)在所有修改后G=H。下方是Meek预测修改边(添加、反向)的具体算法,其中输入是DAG\(\ G\)以及其独立图\(H\),输出是\(G\)修改边后的等价类\(G^{'}\)。

图3 边修正算法
贝叶斯评分标准的渐近行为
我们利用BIC去评价DAG \(G\)相对于预测图\(G^{h}\)的相对后验或者log相对后验,其中\(G\)中的独立性约束与生成式分布结果的独立性约束相同。因此可以利用预测图\(G^{h}\)的log相对后验来构建BIC:
\[\begin{matrix} S_{B}(G,D) = logp\left( G^{h} \right) + \log{p\left( D \middle| G^{h} \right)}\tag{1} \\ \end{matrix}\]
其中\(p(G^{h})\)是\(G^{h}\)的相对先验概率,\(p\left( D \middle| G^{h} \right)\)是边际似然值------衡量\(G^{h}\)和数据\(D\)的拟合程度。此外,BIC评分准则还应具有以下性质:
如果DAG \(H\)符合数据D的分布概率\(p\),而\(G\)不符合,则\(S(H,D) > S(G,D)\)
如果\(H\)和\(G\)均符合,但\(G\)的参数值更少,则\(S(H,D) < S(G,D)\)
因此式(26)的BIC方程可以利用拉普拉斯积分进行近似,因此将式(26)转化为以下形式:
\[\begin{matrix} S_{B}(G,D) = logp\left( D \middle| \ \widehat{\theta},G^{h} \right) - \frac{d}{2}logm + O(1)\tag{2} \\ \end{matrix}\]
其中\(\widehat{\theta}\)是最大似然函数的参数,\(d\)是\(G\)的维度,\(m\)是数据集\(D\)中的数据数量。因此,根据BIC的性质我们可以得到以下结论:DAG模型\(G\)的(1)BIC分数增加来作为添加任何消除独立性约束边的结构,结果图\(G^{'}\)仍然保持在相同的生成分布中,并且(2)减少上述添加的边不会消除这种约束条件。
两阶段的贪婪等价搜索算法
我们使用贝叶斯评分准则\(S_{B}(\varepsilon,D)\)来评价马尔可夫等价类\(\varepsilon\)。如果\(\varepsilon^{*\ }\)表示生成分布P的完美图(数据生成分布P的每一项独立性约束都可以被图表达)的等价类,那么对于其他任图的等价类\(\varepsilon\)均有\(S_{B}\left( \varepsilon^{*},D \right) > S_{B}(\varepsilon,D)\)。
GES算法一共有两个阶段,在第一个阶段中不断添加边来搜索BIC最大的等价类,一旦达到局部最大值则进行第二个阶段,不断减少边,直到BIC再次达到局部最大值,得到最终的因果图。
第一个阶段中,我们使用\(\varepsilon \rightarrow \varepsilon^{+}(\varepsilon) \rightarrow \varepsilon^{'}\),其中\(\varepsilon^{+}(\varepsilon)\)是\(\varepsilon\)的所有相邻等价类,其中\(\varepsilon^{'}\)由\(\varepsilon^{+}(\varepsilon)\)中的一个来修改边得到的,当前仅当从DAG \(G \in \varepsilon\)出发,依据5.3.1.1中的算法,我们可以通过添加单条边达到DAG \(G \in \varepsilon^{'}\)。同样在第二个阶段中,我们进行与第一个阶段相似的删除操作\(\varepsilon \rightarrow \varepsilon^{-}(\varepsilon) \rightarrow \varepsilon^{'}\)。
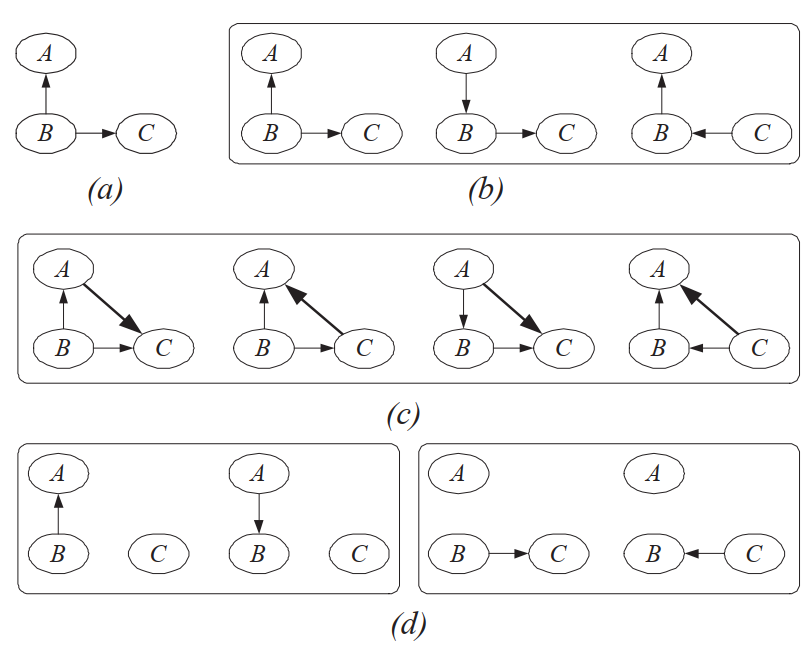
图4 贪婪搜索图
对上述算法进行简要的总结,Meek预测首先描述了在不违反生成分布P的情况下如何对生成图\(G\)的边进行修改;BIC准则描述了对于局部等价类的评分准则是一样的,并且BIC分数的变化不会影响关于生成分布的约束条件。在此基础上提出了GES算法,通过两步贪心操作来得到最终的因果图。
基于结构方程的因果发现(SEM-based or FCM-based Algorithms)
结构方程将结果变量\(Y\)与直接原因变量集合\(X\)和噪声项\(\varepsilon\)用结构方程\(Y = f(X,\varepsilon)\)联系起来,其中\(X\)\(\varepsilon\)相互独立。因果方向的可判定问题是SEM 研究中的一项重要课题,LiNGAM算法研究发现当噪声项服从非 Gauss分布或者函数方程满足非线性约束时,由于原因变量和噪声项间的独立性仅在正确的因果方向下成立,使得变量间的因果方向是可判定的。
LiNGAM算法
LiNGAM作为该研究方向的一个代表性模型, LiNGAM的全称是Linear Non-Gaussian Acyclic Model,即线性非高斯无环模型。它建模连续随机变量间的因果关系,假设变量间线性关联且噪声项服从非 Gauss 分布. 独立成分分析技术(independent component analysis, ICA) 被用于 LiNGAM 的模型选择,但由于超参数选择问题, ICA 算法常常陷入局部最优而无法收敛于最优解。
模型假设
因果单向假设:观测变量\(\{ x_{i}|i \in \{ 1,\ldots,m\}\}\)按一定的因果顺序\(k(i)\)进行排序,在这个排序中,原因变量必在结果变量前面,换句话说,各观测变量的因果图模型必定是有向无环图(DAG,directed acyclic graph),这是因果发现中最基本的假设。
因果充分性假设:在模型中,变量集\(V\)中的任意两个变量的直接原因都存在于\(V\),即不存在未被观测到的混淆变量。这是结构方程模型通用的重要假设之一,如果被观测到的变量集不具有因果充分性,则模型中可能含有未观测到的因变量,从而干扰模型的效果。
数据产生方式假设:
- 数据的生成方式是线性的,原因变量与结果变量之间的函数关系服从线性关系,即:
\[\begin{matrix} x_{i} = \sum_{k(j) < k(i)}^{}{b_{ij}x_{j}} + e_{i} + c_{i}\tag{3} \\ \end{matrix}\]
噪声\(e_{i}\)之间互相独立,这是求解结构方程的前提条件
噪声\(e_{i}\)服从非高斯分布,使得因果模型具有唯一解
基于ICA算法的因果模型识别
独立成分分析(ICA,independent componentanalysis),是近年来出现的一种强有力的数据分析工具,由 Hyvarinen 提出。ICA 又称为盲信号处理,原本是用于从多个混杂的信号中分离出源信号。ICA的目的是将输入的系统的信号\(x(t)\)进行转换,变为相互之间独立的信号\(s(t)\)。 基于非高斯假设,分离出方差相同、服从非高斯分布的源信号。对源信号的非高斯假设是算法的前提,如果源信号服从高斯分布,则可以通过在源信号空间里进行旋转,以得到多个不同的解,只有服从非高斯分布才能得到唯一解。解决线性发现问题的关键是要认识到观测变量是扰动变量的线性函数,且扰动变量相互独立并且非高斯分布的。如果我们对式(28)进行预处理,减去每个变量\(x_{i}\)的平均值,从而可以消除常数项\(c_{i}\),从而将式(28)用矩阵表示为:
\[\begin{matrix} x = Bx + e\tag{4} \\ \end{matrix}\]
其中,\(B\)是表示因果权重的矩阵(通常需要对变量进行排序,使得因果权重矩阵为对角线为零的下三角矩阵),对\(x\)进行求解,我们可以得到下面的方程:
\[\begin{matrix} x = Ae\tag{5} \\ \end{matrix}\]
其中,\(A = (I - B)^{- 1}\),由于\(e\)之间相互独立且服从非高斯分布,于是可以利用ICA求解唯一的\(A\)值,同时得到其逆矩阵\(W = A^{- 1} = I - B\)。此时,求解权重矩阵\(B\)还需要面临两个问题:
由于得到的结果中,源信号的排序是随机的,所以我们需要对\(W\)进行排序使得符合我们的要求(对角线尽量不为零)
通常假设个源信号是服从单位方差的,但实际上在 LiNGAM 中并未对方差做出假设,这样的差异导致的一个结果就是\(W\)的对角线并非全为一。根据\(B\)因果权重矩阵的性质以及因果单向假设,\(W\)的对角线必须全为一,ICA的结果并不满足这一要求。
因此,需要对\(W\)进行如下变换:
对\(W\)进行排序得到对角线不为零的矩阵\(\overset{\sim}{W}\)
对\(\overset{\sim}{W}\),每一行都除以对角元素,得到对角线为一的矩阵\({\overset{\sim}{W}}^{'}\)
因此,基于上述原理,LiNGAM的全局算法流程如下:
对于输入的数据矩阵\(X(m \times n,m \ll n)\),其中一列为一个样本向量\(x\),先进行归一化(除以每一行的均值),以消去其偏置;利用 ICA 算法对\(X = AS\)进行求解,得到相互独立的非高斯噪声\(S\),以及矩阵\(A\),并求得其逆矩阵\(W\);
对\(W\)进行排序得到对角线不为零的矩阵\(\overset{\sim}{W}\),为了方便计算,可将问题转化为:\(\min_{\overset{\sim}{W}}{\sum_{i}^{}\frac{1}{|\overset{\sim}{W_{ii}}|}\ }\)
对\(\overset{\sim}{W}\),每一行都除以对角元素,得到对角线为一的矩阵\({\overset{\sim}{W}}^{'}\)
估计权重矩阵\(B\),可表示为 \(\widehat{B} = I - {\overset{\sim}{W}}^{'}\ \)
最后,对 \(\widehat{B}\)安装因果关系排序,可表示为\(\overset{\sim}{B} = P\widehat{B}P^{T}\),其中\(\overset{\sim}{B}\)接近于一个严格的下三角矩阵,由于通常情况下\(\widehat{B}\)的元素均不为零,问题可以转化为最大化\(\sum_{i \leq j}^{}{\overset{\sim}{B}}_{ij}^{2}\)
基于DL\RL的因果结构发现
独立因果机制(Independence Causal Machanism,ICM
在利用DL\RL进行因果推断以前,我们需要对变量间的因果关系进行一个描述,从而保证式(2)的因果分解是有意义的。在噪声独立的情况下,根据因果图对联合分布进行因果分解总是可行的,因此需要考虑式(2)中因子的独立机制:
一个系统的变量的因果生成过程是由一系列自主模块构成,它们不会影响彼此,也无法提供彼此的信息
改变(干预)一个机制\(P(X_{i}|{PA}_{i})\),不会改变其他机制\(P(X_{j}|{PA}_{j})(i \neq j)\)
知道其他机制\(P(X_{i}|{PA}_{i})(i \neq j)\)不会提供\(P(X_{j}|{PA}_{j})\)的任何信息
我们通常认为现实世界的分布都是因果机制的产物,这种分布的变化,将总是由于至少一个机制的变化。我们首先考虑一个因果的因子化,假设较小的变化往往以一种稀疏或局部的方式表现出来,即它们通常不应该同时影响所有因素,将此类因果分解称为独立因果分解;相反,如果我们考虑一个非因果的因子化,那么当我们改变负责系统统计依赖性的物理机制之一时,许多项将同时受到影响,这样的因式化可以称为纠缠因果分解(entangled )。
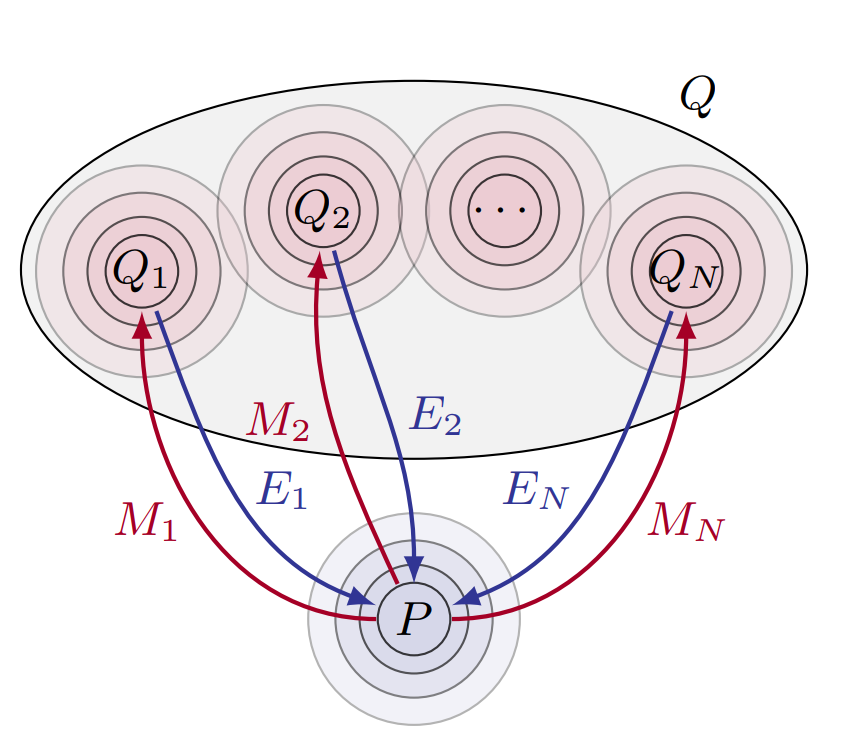
图5 一个生成式分布P由多个独立因果机制Q构成
此外,机制之间的依赖性(Measures of dependence of mechanisms)与随机变量的统计依赖性并不一致。在一个因果图中,即使机制\(p(X_{i}|{PA}_{i})\)和\(p(X_{j}|{PA}_{j})\)是独立的,随机变量\(X_{i}\)和\(X_{j}\)之间也可能存在依赖性。同样,噪声\(U_{i}\)的独立性也与\(X_{i}\)的独立性无关。直观来讲,噪声项\(U_{i}\)提供并参数化了机制\(P(X_{i}|{PA}_{i})\)中的不确定性,并且保证了不同机制存在相互独立的不确定性。在这种意义上,ICM原则包含了在SCM的特殊情况中------如果噪声项不独立,因果机制就不独立了。
基于DL的因果发现
深度学习模型凭借其强大的表征能力在图像分类,语音识别等领域展现巨大的预测能力,但由于其经常将相关性关系认为因果关系,因此可能会对政策制定、行为决策等造成灾难性后果。近来,存在利用神经网络构建因果关系的新发展趋势,如CGNN模型构建了一个生成式网络,通过反向传播训练来最小化观测数据和生成数据之间的最大平均差异(MMD)。该方法建立在5.4的基础上,利用神经网络来拟合结构方程\(X = f({PA}_{X},\varepsilon)\)。通过考虑分布不对称性和条件独立性,解决了双变量和多变量以及混杂因素的情况,不仅估计隐藏在数据下的因果图,而且估计数据的联合概率分布。
生成式因果神经网络(Causal generative neural networks)
该类方法的原理在于将因果图\(\mathcal{G}\)表示为生成式概率分布\(P(X),X \in (x_{1},..,x_{d})\),基于独立因果机制和因果模型的乘积法则可分解为\(\prod_{i = 1}^{}{P(x_{i}|pa_{i})}\)。通过观察因果图模型和结构方程,我们可以利用一系列网络 \(\widehat{f} = (\widehat{f_{1}},\ldots,\widehat{f_{d}})\)来表达生成式分布 \(\widehat{P}\),其中神经网络被定义为 \(\widehat{X_{i}} = \widehat{f_{i}}({\widehat{X}}_{Pa(i:G)},E_{i})\),\(E_{i}\sim\varepsilon\)。
CGNN利用神经网络拟合的数据分布来近似真实的数据分布,因此损失函数就可以被定义为两类分布之间的差,网络的目标就是最小化这个损失函数,损失函数表达为:
\[\begin{matrix} S\left( \widehat{G},D \right) = - {\widehat{MMD}}_{k}\left( D,\widehat{D} \right) - \lambda\left| \widehat{G} \right|\tag{6} \\ \end{matrix}\]
其中\(|\widehat{G}|\)是 \(\widehat{G}\)的edge个数,其中\(MMD\)表示为如下公式:
\[\begin{matrix} {\widehat{MMD}}_{k} = \frac{1}{n^{2}}\sum_{i,j = 1}^{n}{k\left( x_{i},x_{j} \right) + \frac{1}{n^{2}}\sum_{i,j = 1}^{n}{k\left( {\widehat{x}}_{i},{\widehat{x}}_{j} \right) - \frac{2}{n^{2}}\sum_{i,j = 1}^{n}{k\left( x_{i},{\widehat{x}}_{j} \right)}}}\tag{7} \\ \end{matrix}\]
式(32)中\(k\)是高斯核函数,用来衡量距离,\(MMD\)用来衡量两个分布的接近程度。本质上是将FCM与Score-based的思想结合起来,利用神经网络拟合\(f({PA}_{x},E_{x})\)的值,用\(S(\widehat{G},D)\)衡量每条因果方向边的打分,通过不同因果方向的打分来区分马尔可夫等价类。CGNN的具体实现思路如下:
首先输入一个因果框架,即先验无向因果图,这个图一般由专家知识得到,CGNN之后采取和score-based相似的搜索策略,一共有三步:
对于相邻变量\(X_{i}\)和\(X_{j}\),通过两个变量做一个成对反向CGNN,然后两个方向分别训练的,得到最优损失,选择较小的损失作为因果方向
顺着目前因果图的任意一个节点,寻找是否成环,有则反转,保证最终的是无环图
对于目前的图,不断反转某个边然后再训练,如果最后损失减少则接受当前反转。
对于可能存在的混杂因素,将FCM方程扩展为\(X_{i} \leftarrow f_{i}(X_{pa(i;G)},E_{i,Ne(i:s)},E_{i})\),其中\(Ne(i;S) \in \{ 1,\ldots,d\}\)是\(X_{i}\)相邻变量的下标指数。每一个\(E_{i,j}\sim\varepsilon\)代表了\(X_{i},X_{j}\)的共因。因此,当考虑混杂变量时,就把噪声也作为独立变量放进图中进行训练。
基于RL的因果发现
强化学习是机器学习中更为接近因果研究的一个领域,它常常会直接有效的估计do-probabilities,即干预效果。例如on-policy学习就直接估计当前策略干预的do-probabilities。但当涉及off-policy学习或者离线强化学习时,与因果相关的问题就变得十分精妙。强化学习和因果结合的可以大致分为两类:一是在强化学习中结合因果发现,例如智能体可以学到环境的因果模型;二是学习利用因果模型进行规划和行动。已经有越来越多的证据表明,使用恰当的结构化表征是很有帮助的。利用强化学习来进行因果关系的挖掘非常直观,因为智能体的每一个动作都可以看作一个干预,而环境给予的奖励可以看作因果图的分数。基于这个思路,华为诺亚实验室给出了结合强化学习Actor-Critic算法和Score-based因果发现算法的模型。
自编码器式强化学习算法[14]
尽管如5.3.1的基于评分的因果发现算法在有限样本和特定模型假设上取得了很好的成果,但仍陷于条件独立假设的诸多假设而不能适应诸多场景。因此本文利用强化学习来寻找最好评分的DAG,其自动编码器模型将观测数据作为输入,将因果图邻接矩阵作为输出,其中图的评分综合了先验评分函数(BIC)和两项保证无环性的惩罚项。与普通RL不同的是,本模型将图的评分作为最大奖励,并将最终因果图作为输出。
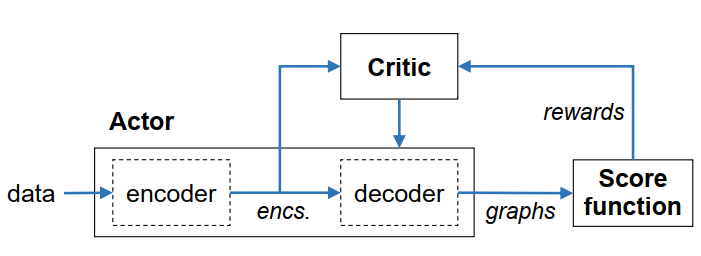
图6 基于RL的自动编码器因果发现模型
评分函数、无环性和奖励
评分函数
在本文中,我们采用BIC作为先验分数函数,有向图\(\mathcal{G}\)的BIC指标定义如下:
\[\begin{matrix} \mathcal{S}_{BIC}\left( \mathcal{G} \right) = - 2logp\left( X;\widehat{\theta}\mathcal{,G} \right) + d_{\theta}logm\tag{8} \\ \end{matrix}\]
其中\(\theta\)是最大似然估计的参数,\(d\)是参数的维度,当我们假设噪声是\(i.i.d\)高斯加性噪声并且方差相同时,式(33)可以转化为下式:
\[\begin{matrix} \mathcal{S}_{BIC}\left( \mathcal{G} \right) = mdlog\left( \frac{\sum_{i = 1}^{d}{RSS_{i}}}{md} \right) + elogm \\ \end{matrix} \tag{9}\]
其中\(RSS = \sum_{k = 1}^{m}\left( x_{i}^{k} - {\widehat{x}}_{i}^{k} \right)^{2}\),表示第\(i\)个变量与真实分布的残差值,\(e\)表示边的数量。式(34)的第一项用来衡量生成图分布与真实数据分布的距离,第二项作为惩罚项对边的数量进行惩罚。
无环性
如何保证因果图的无环性约束?在GES算法中,在添加每条边时显式地检查是否保证无环,在本算法中,可以在打分函数中通过添加惩罚项来保证无环。根据图论,如果邻接矩阵满足\(h(A) = trace\left( e^{A} \right) - d = 0\),则邻接矩阵无环。但是该值可能很小,导致我们需要在惩罚项中添加一个较大的权重并遍历所有DAG,因此我们可以通过一个指示函数来优化该惩罚项。
奖励
奖励函数综合了分数函数和无环性约束,定义为如下公式:
\[\begin{matrix} reward = - \left\lbrack \mathcal{S}\left( \mathcal{G} \right) + \lambda_{1}I\left( \mathcal{G \notin}{DAG}_{s} \right) + \lambda_{2}h(A) \right\rbrack\tag{10} \\ \end{matrix}\]
同时,由于\(\mathcal{S(G)}\)和无环性约束的范围不一样,需要把\(\mathcal{S}\)约束到特定的范围\(\mathcal{S}_{0}\frac{\mathcal{S -}\mathcal{S}_{L}}{\mathcal{S}_{U} - \mathcal{S}_{L}}\),因此最佳得分的范围在\(\lbrack 0,\mathcal{S}_{0}\rbrack\)。我们令\(\pi(.|s)\)表示策略,令\(\psi\)表示神经网络参数,因此我们的预期奖励被定义为如下公式:
\[\begin{matrix} J\left( \psi \middle| s \right) = E_{A\sim\pi\left( . \middle| s \right)}\left\{ - \left\lbrack S\left( \mathcal{G} \right) + \lambda_{1}I\left( \mathcal{G \notin}DAG_{s} \right) + \lambda_{2}h(A) \right\rbrack \right\}\tag{11} \\ \end{matrix}\]
综合6.3.2.1-6.3.2.3的讨论,该RL算法的具体流程如下:

图7 基于自动编码器RL算法流程
既然我们最后的输出是一个拥有最好评分的DAG而非策略,因此最终的输出图可能包含许多虚假边,因此剪枝仍是必要的。在接下来的步骤中,采用GES算法第二步相似的操作,对于有因果关系的双变量,通过移除父变量来衡量结果图的表现,如果因果关系没改变则保留该次剪枝操作。对于线性系统,剪枝可通过简单地为估计系数设定阈值来实现。
总结来说,本算法利用Actor-Critic框架来构建RL算法,其中Actor采用了自编码器模型,Critic采用了双层前向反馈神经网络,奖励通过整合先验分数函数和无环性约束来保证因果图的正确性。
参考文献
[1] 苗旺, 刘春辰, 耿直. 因果推断的统计方法. 中国科学(数学), 2018,48(12):1753-1778.
[2] Pearl J. Causal inference in statistics: An overview. Statistics Surveys, 2009, 3(none).
[3] Pearl J, Glymour M, Jewell N P. Causal inference in statistics: A primer: John Wiley & Sons, 2016.
[4] Glymour C, Zhang K, Spirtes P. Review of Causal Discovery Methods Based on Graphical Models. Front Genet, 2019, 10.
[5] Ramsey J, Glymour M, Sanchez-Romero R, et al. A million variables and more: the Fast Greedy Equivalence Search algorithm for learninghigh-dimensional graphical causal models, with an application to functional magnetic resonance images. International Journal of Data Science and Analytics, 2017, 3(2):121-129.
[6] Spirtes P, Glymour C. An Algorithm for Fast Recovery of Sparse Causal Graphs. Soc Sci Comput Rev, 1991, 9(1):62-72.
[7] Spirtes P, Glymour C N, Scheines R, et al. Causation, prediction, and search: MIT press, 2000.
[8] Chickering D M. Optimal structure identification with greedy search. J Mach Learn Res, 2002, 3(Nov):507-554.
[9] Harada K, Fujisawa H. Sparse estimation of Linear Non-Gaussian Acyclic Model for Causal Discovery. Neurocomputing (Amsterdam), 2021, 459:223-233.
[10] Parascandolo G, Kilbertus N, Rojas-Carulla M, et al. Learning Independent Causal Mechanisms. 2017.
[11] Schölkopf B. Causality for Machine Learning. 2019.
[12] Scholkopf B, Locatello F, Bauer S, et al. Toward Causal Representation Learning. P Ieee, 2021, 109(5):612-634.
[13] Goudet O, Kalainathan D, Caillou P, et al. Causal Generative Neural Networks. 2018.
[14] Zhu S, Ng I, Chen Z. Causal discovery with reinforcement learning. arXiv preprint arXiv:1906.04477, 2019.