地理加权回归模型
引言
空间异质性是地理学第二定律的核心。从地理信息科学角度,空间异质性主要包含两种类型,一是随空间变化,空间某些变量之间的关系发生了明显变化;二是随空间变化,空间某些变量的统计量(如:均值、方差)会出现平稳或者不平稳的变化。地理加权回归是空间计量学、地理空间统计学中为研究第一种空间异质性(即变量间关系的空间异质性)而提出的工具,在多元变量的空间插值或预测等方面具有重要作用。本文为相关原理的基本介绍。
全局空间最小二乘回归问题
在地学空间分析中,n组观测数据通常是在n个不同地理位置上获取的样本数据,全局空间回归模型就是假定回归参数与样本数据的地理位置无关,或者说在整个空间研究区域内保持稳定一致,那么在n个不同地理位置上获取的样本数据,就等同于在同一地理位置上获取的n个样本数据,其回归模型就是最小二乘法回归模型,采用最小二乘估计得到的回归参数户既是该点的最优无偏估计,也是研究区域内所有点上的最优无偏估计。
而在实际问题研究中我们发现:回归参数在不同地理位置上往往表现为不同,也就是说回归参数随地理位置变化而变化,存在空间非平稳性,此时如果仍采用全局空间回归模型,得到的回归参数将是在整个研究区域内的参数平均值,无法反映回归参数的真实空间特征。
分析空间非平稳性
目前,空间非平稳性的分析方法已经有了很多。其中针对某些变量之间关系的空间异质性问题,有如下方法:
广义最小二乘法。该方法把回归模型的参数转化成地理空间位置的线性函数,利用模型参数的线性函数得到模型的参数估计,模型参数随空间位置的变化而变化。该方法在参数变化十分复杂的情况下的应用受到一定限制。
空间滤波方法。该方法借鉴时间序列分析中利用 "预测 --- 修正" 原理来补偿参数漂移的思路,将其应用到空间数据中来分析回归参数的漂移,用迭代计算来估计参数。该方法局限性是其参数估计不能够做统计检验。
随机系数模型。假设回归模型的系数为随机变量,相互独立且为有限混合分布,基于贝叶斯原理和最大似然法来估计参数的概率。
多层次模型。假设回归模型的系数为随机变量,相互独立且呈正态分布,基于贝叶斯原理和最大似然法来估计参数的概率。
地理加权回归模型的提出
为解决该问题,国外有学者提出了空间变参数回归模型(Spatially Varying-Coefficient Regression Model),将数据的空间结构嵌入回归模型中,使回归参数变成观测点地理位置的函数。Fortheringham等在空间变系数回归模型基础上利用局部光滑思想,提出了地理加权回归模型(Geographieally Weighted Regression Model, GWR)。
基础模型
地理加权回归模型(GWR)是对全局线性回归模型的扩展。该模型将样本点的地理位置嵌入到回归参数之中,即:
\[\begin{matrix} y_{i} = \beta_{0}\left( u_{i},v_{i} \right) + \sum_{k = 1}^{p}{\beta_{k}\left( u_{i},v_{i} \right)x_{ik} + \epsilon_{i}}\ i = 1,2,\ldots,n\ \tag{1} \\ \end{matrix}\]
式(1)中:\((u_{i},v_{i})\)为第i个样本点的坐标;\(y_{i}\)为第i个样本点的因变量观测值;\(x_{ik}\)为第i个样本点的第k个自变量,\(\beta(u_{i},v_{i})\)是在第i个样本点处第k个自变量的权重;p为自变量个数;n为样本总数;\(\epsilon_{i}\)为第i个样本点的随机误差。可将(1)式简写为如下形式:
\[\begin{matrix} y_{i} = \beta_{0} + \sum_{k = 1}^{p}{\beta_{k}x_{ik} + \epsilon_{i}}\ i = 1,2,\ldots,n\ \tag{2} \\ \end{matrix}\]
该式意味着:对于样本集合中的每个样本点,地理加权回归模型都将利用所有样本为其构建一个线性回归模型,所以GWR模型的参数总量是全局加权回归模型的n倍。若全局加权回归模型的参数为(p+1)个,则GWR的模型参数为\(n \times (p + 1)\)个。当所有样本点的模型参数一致时,地理加权回归模型就退化为全局加权回归模型。
空间自相关性和异质性的体现
依据地理加权回归模型的基本原理,使用所有样本来为每一个样本点生成一套权重系数,而根据地理学第一定律,距离目标点越远的样本,对目标因变量的影响越小,因此可以在每个样本点的地理加权回归模型参数中嵌入空间结构要素,来体现该空间自相关性。而不同样本点具有不同的回归模型参数,则体现了地理学第二定律的空间异质性原则。
由此可见,地理加权回归模型的关键是如何将空间结构要素嵌入到回归模型的参数中。Fotheringham 等(1996)在传统最小二乘法基础上,通过加入空间权重矩阵\(W\)的方式,实现空间结构要素的嵌入。每个目标点的\(W\)不同,体现了空间异质性,而矩阵内权重的大小(根据地理学第一定律,通常受距离影响),体现了自相关程度。
\[\begin{matrix} 传统最小二乘:\widehat{\beta}\left( u_{i},v_{i} \right) = \left( X^{T}X \right)^{- 1}X^{T}Y\ \tag{3} \\ \end{matrix}\]
\[\begin{matrix} 地理加权最小二乘:\widehat{\beta}\left( u_{i},v_{i} \right) = \left( X^{T}W\left( u_{i},v_{i} \right)X \right)^{- 1}X^{T}W\left( u_{i},v_{i} \right)Y\ \tag{4} \\ \end{matrix}\]
其中: \(\widehat{\beta}\)是模型参数\(\beta\)的估计值,\(n\)是空间样本点数,\(p\)是自变量个数,\(W_{ik}\)是对位置\(i\)刻画模型时赋予第\(k\)个样本的权重。由此可见,对于地理加权回归模型来说,关键是如何计算空间权重矩阵\(W\)(空间权重矩阵量化描述了\(n\)个空间位置之间相互的关系)。由于地理加权回归模型中的回归参数在各采样点上均不同,因此其未知参数的个数为\(n \times (p + 1)\),远大于观测样本个数\(n\),采用传统参数估计方法同时计算未知参数比较困难,因此有学者提出了一些方法来拟合该模型。
Foste & Gorr(1986)和 Gorr & Olligsehiaeger(1994)利用广义阻尼负反馈(generalized damped negative feedback)方法估计未知参数在各地理位置的值,该估计方法只是在很直观的意义上考虑数据的空间结构,加之估计方法较为复杂,很难对估计量作深入的统计推断方面的研究。
Brunsdon 等(1996)在局部多项式光滑思想上提出了偏差和方差折衷(Bias-Variance Trade-off)的解决思路:假设回归参数为一连续表面,位置相邻则回归参数非常相似,在估计采样点i的回归参数时,以采样点i及其邻域采样点上的观测值构成局域子样本,建立全局线性回归模型,然后采用最小二乘方法得到回归参数估计 \({\widehat{\beta}}_{ik}\)。对于另一个采样点\(i + 1\),采用另一个相应的局域子样来估计,以此类推。由于在回归过程中,由其它样点上的观测值来估计点上的模型参数,因此\(i\)点上的参数估计不可避免存在偏差,为有偏估计。而且,参与回归估计的子样规模越大,参数估计的偏差就越大,反之,参与回归估计的子样规模越小,参数估计的偏差就越小。从降低偏差角度考虑应当尽量减少子样规模,但子样规模的减少必然导致回归参数估计值的方差增加,精度降低。
空间权函数的选择
空间权重矩阵是地理加权回归模型的核心,而权重是由空间坐标的某种函数(即空间权函数)形式体现的,因此,如何选取空间权函数对地理加权回归模型的参数估计影响很大。常见方法有:
距离阈值法
距离阈值法是最简单的空间权函数,它的关键是选取合适的距离阈值D,然后与每一个数据点j与回归点i之间的距离\(d_{ij}\) 进行比较,若\(d_{ij}\)大于该阈值则权重为0,否则为 1,即:
\[\begin{matrix} w_{ij} = \left\{ \begin{matrix} 1\ d_{ij} \leq D \\ 0\ d_{ij} > D \\ \end{matrix} \right.\ \ \tag{5} \\ \end{matrix}\]
该权重函数实质就是滑动窗口,计算简单但函数不连续,因此较少采用。
距离反比法
Tobler(1970)地理学第一定律认为空间相近的地物比相远的地物具有更强的相关性,因此在估计回归点i的参数时,应对回归点的邻域给予更多的关注。根据该思路,人们自然想到用距离来衡量该空间关系:
\[\begin{matrix} w_{ij} = \frac{1}{d_{ij}^{\alpha}}\ \tag{6} \\ \end{matrix}\]
这里\(\alpha\)为合适的常数,当\(\alpha\)取值为 1 或 2 时,对应的是距离倒数和距离倒数的平方。该方法简洁明了,但对于回归点本身也是样本数据点的情况,就会出现回归点观测值权重无穷大的情况,若从样本中剔除自身又会降低参数估计精度,所以直接采用距离反比法的模型也不多,需要对其修正。
高斯函数法
高斯(高斯)函数法就是表示\(w_{ij}\)与\(d_{ij}\)之间的连续单调递减函数,可以克服上述空间权函数不连续的缺点。其函数形式如下:
\[\begin{matrix} w_{ij} = \frac{1}{\exp\left( 0.5*\left( \frac{d_{ij}}{b} \right)^{2} \right)}\ \tag{7} \\ \end{matrix}\]
式中b是描述权重与距离之间函数关系的非负衰减参数,称之为带宽(Bandwidth)。带宽越大,权重随距离的增加而衰减越慢,带宽越小,权重随距离增加而衰减越快。
bi-square 函数法
实际应用中往往会将对回归参数估计几乎没有影响的样点截掉,不参与计算,从而形成以有限高斯函数来代替高斯函数的模型,最常采用的便是bi-square 函数:
\[\begin{matrix} w_{ij} = \left\{ \begin{matrix} \left\lbrack 1 - \left( \frac{d_{ij}}{b} \right)^{2} \right\rbrack^{2}\ d_{ij} \leq b \\ 0\ {\ \ \ \ \ \ \ \ \ \ \ d}_{ij} > b \\ \end{matrix} \right.\ \ \tag{8} \\ \end{matrix}\]
从上式可以看出,bi-square函数法可以看成是距离阈值法和高斯(高斯)函数法的结合。带宽范围内的回归点,可以通过有限高斯函数来计算数据点的权重,而带宽之外的数据点权重为0。
带宽的确定与优化
在实际应用中发现,地理加权回归分析对高斯权函数和 bi-Square权函数的选择并不是很敏感,但对特定权函数的带宽却很敏感带宽过大回归参数估计的偏差过大,带宽过小又会导致回归参数估计的方差过大。最小二乘平方和是最常采用的优化原则之一,但对于地理加权回归分析中的带宽选择却失去了作用,这是因为对于\(\min\sum_{i = 1}^{n}\left\lbrack y_{i} - {\widehat{y}}_{i}(b) \right\rbrack^{2}\)而言,带宽b越小参与回归分析的数据点权重越小,预测值 \({\widehat{y}}_{i}\)越接近真实观测值\(y_{i}\),从而\(\sum_{i = 1}^{n}\left\lbrack y_{i} - {\widehat{y}}_{i}(b) \right\rbrack^{2} \approx 0\),也就是说最优带宽是只包含一个样本点的狭小区域。为此,科学家给出了多种确定或者优化带宽的方法。
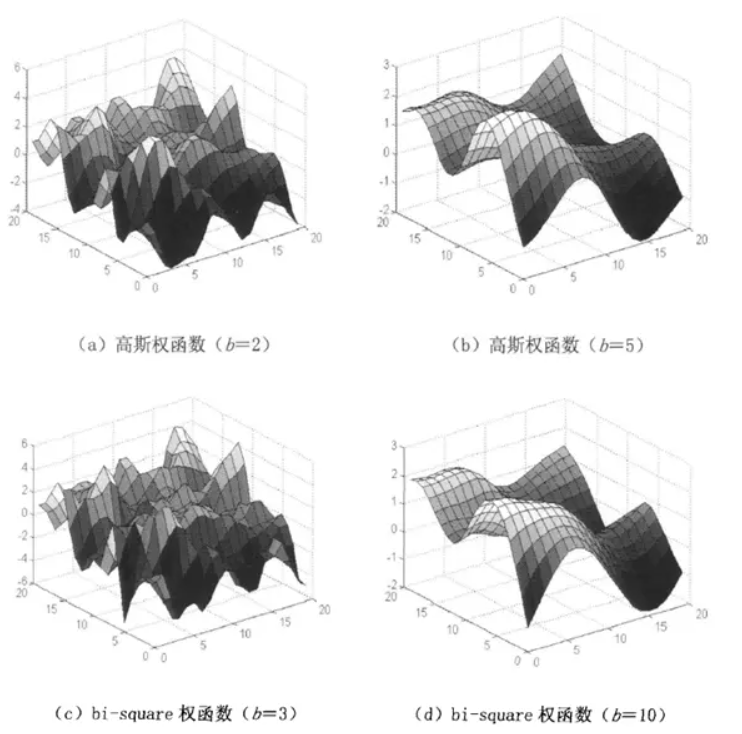
不同权函数与带宽选择对参数估计的影响
交叉验证法
Cleveland (1979)、Bowman(1984)建议采用用于局域回归分析的交叉验证(cross-validation,CV)方法,其公式表达为:
\[\begin{matrix} CV = \sum_{i = 1}^{n}\left\lbrack y_{i} - {\widehat{y}}_{\neq i}(b) \right\rbrack^{2}\ \tag{9} \\ \end{matrix}\]
其中,\({\widehat{y}}_{\neq i}(b)\)是\(y_{i}\)的估计值。该方法在生成 \(\widehat{y}\)时排除了点i的观测值。这样当b变得很小时,模型仅仅刻画点i附近样点而没有包括i本身。把不同的带宽b和相应的CV绘制成趋势线,那么就可以找出CV值最小时,对应的最佳带宽b。
在实际应用中为减少计算量,Loader 于 1999年提出了一种近似交叉验证统计量的方法,称为广义交叉验证方法(generalized cross validation,GCV):
\[\begin{matrix} GCV = \frac{1}{n}\frac{\sum_{i = 1}^{n}\left( y_{i} - {\widehat{y}}_{i}(b) \right)^{2}}{\left( 1 - tr\left( \frac{S(b)}{n} \right) \right)^{2}} = \frac{n\sum_{i = 1}^{n}\left( y_{i} - {\widehat{y}}_{i}(b) \right)^{2}}{(n - tr\left( S(b) \right)^{2}}\ \tag{10} \\ \end{matrix}\]
由KT变换矩阵S的构成可知,当带宽很小时,地理加权回归分析的有效参数个数趋近样本数量n,上式中的分母趋于零,这样即便预测值\({\widehat{y}}_{i}(b)\)趋向\(y_{i}\),GCV也不会等于0。
AIC 准则
Akaikz通过对基于极大似然原理的参数估计方法加以修正,提出了一种较为通用的模型选择准则,称为Akaike 信息量准则(Akaike Information Criterion,AIC)。AIC定义为(Akaike,1974):
\[\begin{matrix} AIC = - 2lnL\left( {\widehat{\theta}}_{L},x \right) + 2q\ \tag{11} \\ \end{matrix}\]
其中, \({\widehat{\theta}}_{L}\)为\(\theta\)的极大似然估计,q为参数个数。AIC准则应用比较广泛,Hurvich et al 将 AIC准则扩展到非参数回归分析中的光滑参数选择,Brunsdon和Fotheringham则在Hurvich等研究基础上将其进一步用于地理加权回归分析中的权函数带宽选择,其公式为:
\[\begin{matrix} {AIC}_{c} = 2nln\left( \widehat{\sigma} \right) + nln(2\pi) + n\frac{n + tr(S)}{n - 2 - tr(S)}\ \tag{12} \\ \end{matrix}\]
其中,下标c表示"修正后的"AIC估计值,n是样点大小, \(\widehat{\sigma}\)是误差项估计的标准差,\(tr(S)\)是GWT的K-T 变换矩阵 S 的迹,它是带宽的函数。AIC有利于评价GWR模型是否比传统最小二乘模型更好地模拟数据。
贝叶斯信息准则
1978 年 SehwartZ 提出了贝叶斯信息准则(Bayesian InformationCriterion,BIC),该准则可以使自回归模型的阶数适中,故常被用来确定回归模型中的最优阶数,2002年 Nakaya 将其用于地理加权回归分析中的权函数带宽选择。BIC 准则与 AIC准则非常相似,只是惩罚因子不同,其公式为:
\[\begin{matrix} BIC = - 2lnL\left( {\widehat{\theta}}_{L},x \right) + qlnn\ \tag{13} \\ \end{matrix}\]
中可以看出,BIC准则对于具有相同未知参数个数的模型,样本数越多,惩罚度越大,对于具有相同样本的情况,则趋于选择具有更少参数的模型为最优。与AIC 不同的是,BIC 准则要求模型为 Bayesian模型,即每个候选模型都必须具有相同的先验概率,而实际上模型参数的先验分布通常是不知道的,另外如何将BIC准则扩展到可变带宽的非参数模型,用有效参数个数来代替全局参数个数还不是很清楚。
参考文献
BRUNSDON C, FOTHERINGHAM AS, CHARLTON M. Geographically weighted regression: A method for exploring spatial nonstationarity[J].Geographical Analysis, 1996, 28(4): 281 2298.
BRUNSDON C, FOTHERINGHAM AS, CHARLTON M. Spatial nonstationarity and autoregressive models[ J]. Environment and Planning A, 1998, 30:957 2973.
HUANG Yefang, LEUNG Yee. Analysing regional industrialisation in Jiangsu province using geographically weighted regression [J]. J Geograph Syst, 2002, 4: 233 2249.
PARK Nokil. Estimation of average annual daily traffic (AADT) using geographically weighted regression (GWR) method and geographic information system (GIS)[R]. Florida: Florida International University, Doctor Dissertation, 2004.
ANTONIO Paez, TAKASHI Uchida, KAZUAKI Miyamoto. A general framework for estimation and inference of geographically weighted regression models: Location- specific kernel bandwidths and a test for locational heterogeneity[J]. Environment and Planning A, 2002, 34: 7332745, 883 2904.