概率图模型
介绍
概率图模型(PGM,probabilistic graphical model)是一种用于学习这些带有依赖的模型的强大框架。概率图模型(或简称图模型)在形式上是由图结构组成的。图的每个节点都关联了一个随机变量,而图的边则被用于编码这些随机变量之间的关系。概率图模型可以简单的理解为"概率+结构",即利用图模型来结构化各变量的概率并有效、清晰的描述变量间的相互依赖关系,同时还能进行高效的推理,因此在机器学习中概率图模型是一种应用广泛的方法。
根据图是有向的还是无向的,可以将图的模式分为两大类------贝叶斯网络和马尔可夫网络。依据目的,可以将学习方法分为基于已知网络结构的参数学习与基于观测数据的结构学习。根据模型的复杂程度,可以将推断方法分为精确推断与近似推断两大类。整个模型的理论架构如图1所示:
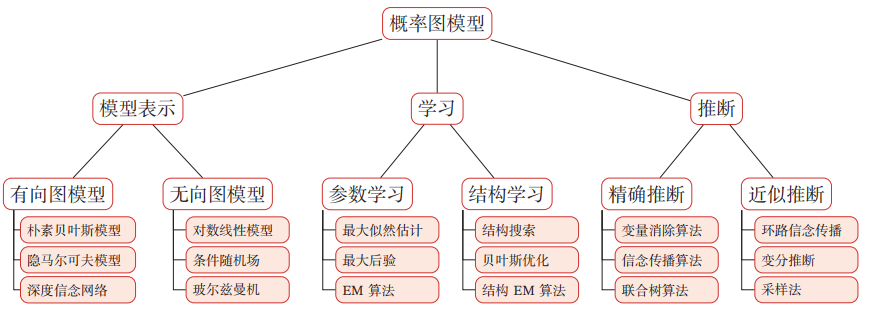
图1 概率图模型概览
有向图模型
贝叶斯网络
贝叶斯网络本质上可以表示任何完全联合概率分布,其完整的定义如下:
每个结点对应一个连续或离散的随机变量
一组有向边连接点对,如果有向边\(X\)指向\(y\)即\(x \rightarrow y\),则称\(x\)为\(y\)的一个父节点
通过条件分布概率\(P(x_{i}|Parents(x_{i}))\)刻画父节点\(Parents\)对\(x_{i}\)的影响
图中不存在任何回路,因此成为有向无环图(DAG)
条件独立性
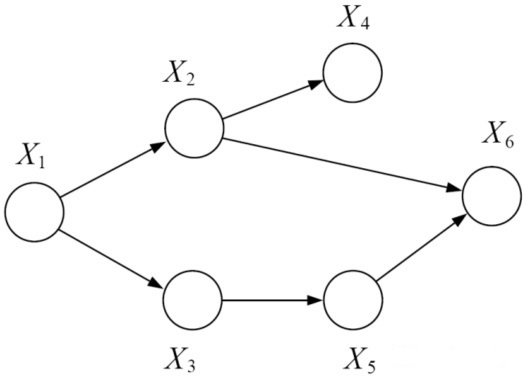
图2 条件独立性
基于图模型,上图的联合概率分布可表示为如下所示:
\[\begin{matrix} P\left( x_{1},x_{2},x_{3},x_{4},x_{5},x_{6} \right) = P\left( x_{1} \right)P\left( x_{2} \middle| x_{1} \right)P\left( x_{3} \middle| x_{1} \right)P\left( x_{4} \middle| x_{2} \right)P\left( x_{5} \middle| x_{3} \right)P\left( x_{6} \middle| x_{2},x_{5} \right)\ \tag{1} \\ \end{matrix}\]
对于有向无环图,若给定一个节点\(x_{i}\)的父节点\(x_{\pi i}\),该节点和其祖先节点(除去父节点)条件独立,即\(x_{4}\bot x_{1},x_{3}|x_{2}\)。
无向图模型
马尔可夫随机场
与有向图不同的是无向图各个变量间没有显示的因果关系,因此我们通过无向的边连接。在有向图中我们可以根据三个基本的结构(或d-分隔)来判断两变量间是否条件独立即两个结点路径是否被"阻隔",在无向图只要图中存在至少一条路径未被"阻隔"则条件独立性均未必成立。我们定义马尔可夫毯如下图所示:
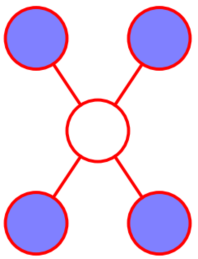
图3 马尔可夫毯
团与极大团
在一个无向图中,结点\(x_{i}\)的马尔可夫毯由相邻结点的集合组成,对于结点\(x_{i}\)其只条件依赖于相邻结点,而条件独立于任何其他的结点。此外在有向图中我们可以依赖每个变量条件概率求解联合概率,而在无向图中由于失去了变量间的因果指向关系,其并不对应一个条件分布,因此通过局部参数表示联合概率将会面对一致性问题。对此我们根据朴素图理论分割引入团的概念。
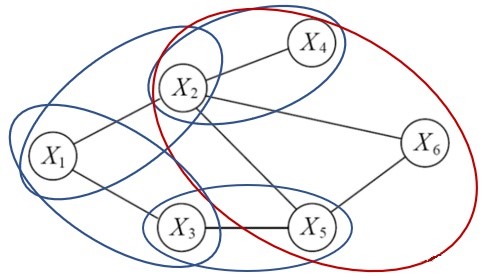
图4 团与极大团
图上的团是一个完全连接的节点子集,也即局部函数的定义域。为了不失一般性我们引入极大团,极大团不为任何其他团的子集。上图中椭圆围住的结点即为极大团。
Hammerseley-Clifford定理
对于N个变量的马尔可夫随机场,其变量为\(X = (X_{1},X_{2},\ldots,X_{n})\)(图四中N=6)。此时联合概率分布即可分解为多个团势能函数的乘积,每个势函数仅与一个团相关。假设所有团构成的集合为\(C\),与团\(Q \in C\)对应的变量集合记为\(X_{Q}\),则联合概率分布如下式所示:
\[\begin{matrix} P(X) = \frac{1}{Z}\prod_{Q \in C}^{}{\phi_{Q}\left( X_{Q} \right)}\ \tag{2} \\ \end{matrix}\]
其中\(\phi_{Q}\)为团\(Q\)的势函数,用于对团\(Q\)中的变量关系进行建模。\(Z\)为规范化因子,为了保证\(P\)的范围有意义,很多时候计算它很困难,不过好在大多数情况下,我们无须计算出\(Z\)的精确值。当\(Q\)不是极大团的时候,它必然属于某个极大团,此时可以完全利用极大团来计算:\(P(X) = \frac{1}{Z^{*}}\prod_{Q \in C^{*}}^{}{\phi_{Q}(X_{Q})}\),其中\(C^{*}\)为所有极大团的集合。
这叫做Hammersley-Clifford定理,是随机场的基础定理,它给出了一个马尔可夫随机场被表达为正概率分布的充分必要条件。
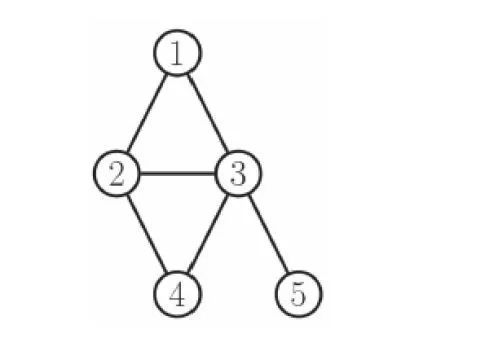
图5 马尔可夫随机场
对于图5表达的马尔可夫随机场,其联合概率分布表达式为:
\[\begin{matrix} p\left( y \middle| \theta \right) = \frac{1}{Z(\theta)}\phi_{123}\left( y_{1},y_{2},y_{3} \right)\phi_{234}\left( y_{2},y_{3},y_{4} \right)\phi_{35}\left( y_{3},y_{5} \right)\ \tag{3} \\ \end{matrix}\]
分离集
设A、B、C都是马尔可夫随机场中的节点,若从A中的节点到B中的节点都必须经过C中的节点,则称A和B被C分离,C成为分离集,如下图所示:
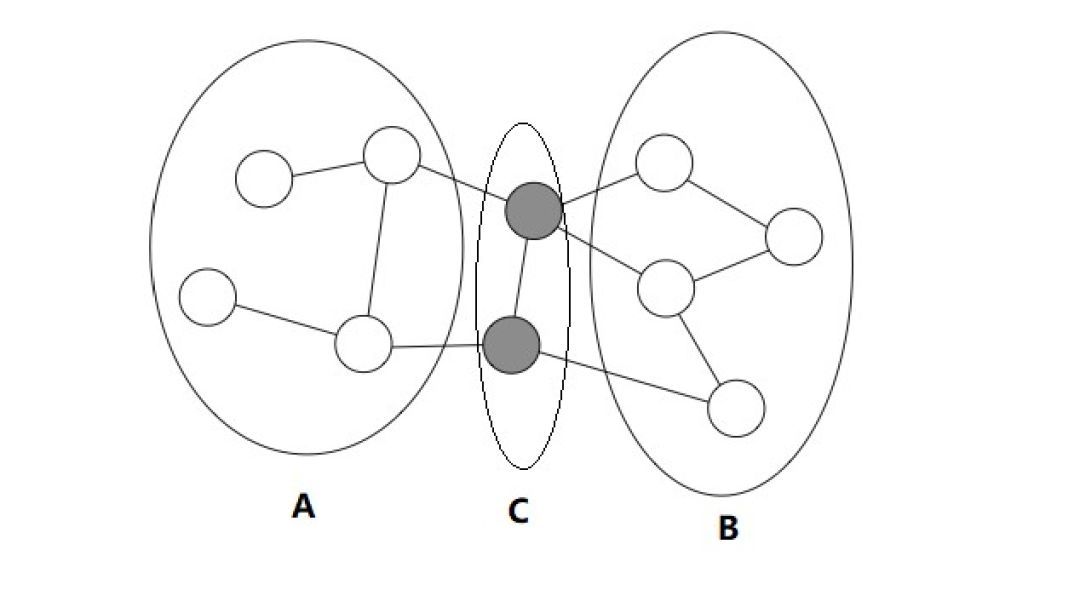
图6 分离集
于是,对于上图表达的马尔可夫随机场,由Hammersley-Clifford定理可得联合概率为:
\[\begin{matrix} P\left( x_{A},x_{B},x_{C} \right) = \frac{1}{Z}\phi_{AC}\left( x_{A},x_{C} \right)\phi_{BC}\left( x_{B},x_{C} \right)\ \tag{4} \\ \end{matrix}\]
马尔可夫性
全局马尔可夫性:设结点集合A,B是在无向图G中被结点集合C分开的任意结点集合,则在给定随机变量\(X_{C}\)的条件下,随机变量\(X_{A}\)和\(X_{B}\)条件独立。
局部马尔可夫性:设v是无向图G中任意一个结点,W是与v有边相连的所有结点,G中其他结点记做O;则在给定随机变量\(X_{W}\)的条件下,随机变量\(X_{V}\)和\(X_{O}\)条件独立。此时这里的W是v的分离集,局部马尔可夫性是全局马尔可夫性的推论。
成对马尔可夫性:设u和v是无向图G中任意两个没有边直接连接的结点,G中其他结点的集合记做O;则在给定随机变量\(X_{O}\)的条件下,随机变量\(X_{U}\)和\(X_{V}\)条件独立。
势函数的选择
马尔可夫随机场有一组势函数,也称为因子。势函数是定义在变量子集上的非负实函数,主要用于定义概率分布函数。势函数的作用是定量刻画变量集\(X_{Q}\)中变量之间的相关关系,它应该是非负函数,且在所偏好的变量取值上有较大的函数值。为了满足非负性,定义势函数通常采用指数函数:
\[\begin{matrix} \phi\left( X_{Q} \right) = e^{- H_{Q}\left( x_{Q} \right)}\ \tag{5} \\ \end{matrix}\]
\(H_{Q}(x_{Q})\)是一个定义在变量\(x_{Q}\)上的实值函数,常见形式为:
\[\begin{matrix} H_{Q}\left( x_{Q} \right) = \sum_{u,v \in Q,u \neq v}^{}{a_{uv}x_{u}x_{v}} + \sum_{v \in Q}^{}{\beta_{v}x_{v}}\ \tag{6} \\ \end{matrix}\]
学习与推断
通过概率图模型我们得到了唯一的联合概率分布,通过联合概率分布我们一般可以计算变量的边际概率分布和条件概率分布,其中计算条件概率分布的过程即对应推断任务。在推断任务中我们是假定图结构固定已知,另一类问题则需要我们从数据出发而推断图本身,即结构学习。
一般图结构学习均采用贪心搜索的策略,即定义可能结构的空间和用于对每个结构评分的度量,通过评分奖励精度高的结构,同时对结构的复杂度做出惩罚,然后添加或移除少量边进行下一步搜索。同时由于图结构的复杂度随结点数目的增加而呈指数增长,因此我们需要借助启发式的方法。根据贝叶斯学派的观点,基于数据\(D\)推断合理的图模型\(M\),其本质是在求解后验概率估计 \(P(M|D)\)。
而对于已知图结构的概率推断人物,其实就是在给定某个已观测的事件后,计算查询变量的后验概率分布,其一般可分为精确推断(变量消去、信念传播)和近似推断(采样、变分推断)的方法
精确推断
变量消去法
变量消去法也称为枚举法,即利用概率的乘法公式和求和或积分操作计算目标变量的概率。变量消除法的思想很简单,就是对联合概率不断求和消除其中的变量,最后得到边缘分布。如下图所示,首先对联合概率来说,先把b消元,得到中间只含a和c的表,然后对c进行求和,得到最后只含有a的概率表,对这个表进行归一化之后,就得到了a的概率。
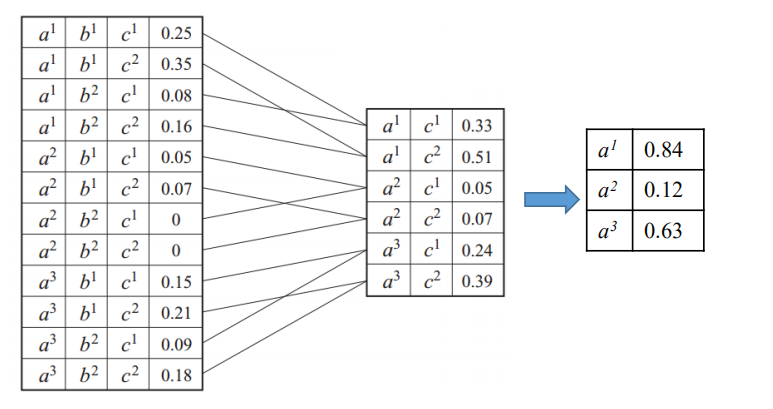
图7 联合概率分布表
以贝叶斯网络为例,给出公式化的表达过程:
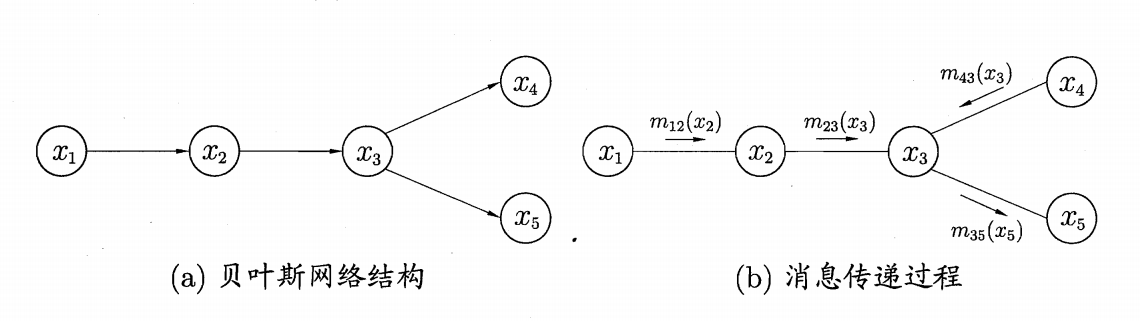
图8 精准推断法
以\(P(x_{5})\)为例,其因子乘积形式为:
\[\begin{matrix} P\left( x_{5} \right) = \sum_{x_{4}}^{}{\sum_{x_{3}}^{}{\sum_{x_{2}}^{}{\sum_{x_{1}}^{}{P\left( x_{1} \right)P\left( x_{2} \middle| x_{1} \right)P\left( x_{3} \middle| x_{2} \right)P\left( x_{4} \middle| x_{3} \right)P\left( x_{5} \middle| x_{3} \right)}}}}\ \tag{7} \\ \end{matrix}\]
首先对\(x_{1}\)进行消元,过程如下:
\[\begin{matrix} P\left( x_{5} \right) = \sum_{x_{3}}^{}{P\left( x_{5} \middle| x_{3} \right)}\sum_{x_{4}}^{}{P\left( x_{4} \middle| x_{3} \right)}\sum_{x_{2}}^{}{P\left( x_{3} \middle| x_{2} \right)}m_{12}\left( x_{2} \right)\ \tag{8} \\ \end{matrix}\]
上式中,\(m_{ij}(x_{j})\)即为对\(x_{j}\)求加和的中间结果,最终式(8)可简化为\(P\left( x_{5} \right) = m_{35}(x_{5})\)。
信念传播法
消信念传播(Belief Propagation)算法将变量消去算法中的求和操作看做一个消息传递的过程,如下:
\[\begin{matrix} m_{ij}\left( x_{j} \right) = \sum_{x_{i}}^{}{\phi\left( x_{i},x_{j} \right)}\prod_{k \in n(i)\backslash j}^{}{m_{ki}\left( x_{i} \right)}\ \tag{9} \\ \end{matrix}\]
上式中\(m_{ij}(x_{j})\)表示\(x_{i}\)传递至\(x_{j}\)的消息,\(n_{i}\)为\(x_{i}\)的邻近结点,因此每次消息的传递仅与变量\(x_{i}\)及其邻近结点有关,即消息传递的相关计算被限制在图的局部进行,其中结点的边际分布正比于它所接受的消息的乘积:
\[\begin{matrix} P\left( x_{i} \right) = \prod_{k \in n(i)}^{}{m_{ki}\left( x_{i} \right)}\ \tag{10} \\ \end{matrix}\]
变量消去和信念传播算法均为加和-乘积算法。该算法加和乘积的具体顺序和算法的复杂度均由图结构决定,在实际的情况中由于图结构复杂,变量数目庞大精确推断在是不可行的。为此我们需要进行近似推断计算后验概率。
近似推断
马尔可夫链蒙特卡洛采样(MCMC)
在现实的许多情况下我们需要计算某些变量的和或积分时,由于其数目较多直接计算将不可行,这时我们可以引入蒙特卡洛采样的方法,将求和或积分运算转化为求某一特定分布下的期望,进而通过平均值近似期望得到所求结果。此外,如果样本服从i.i.d分布,则在大数定律的前提下,其估计均值必将几乎必然收敛至期望值。这也保证了蒙特卡洛采样的合理性和估计的无偏性。
实际中,\(x\)的取值\(p\)十分复杂,因此积分计算通常非常困难。为避免直接计算可以采用MCMC采用,其核心思想在于通过随机采样获得独立同分布的样本\(x_{1},x_{2},\ldots,x_{n}\),使得其尽可能接近\(p\)分布中的样本,最后得到\(p(x)\)的无偏估计:
\[\begin{matrix} \widetilde{p}(x) = \frac{1}{N}\sum_{i = 1}^{N}x_{i}\ \tag{11} \\ \end{matrix}\]
因此,问题转化为如何使得采样样本足够近似服从\(p\)分布。这里定义\(x\)在\(t\)时刻的状态分布概率为\(p(x^{t})\),状态转移概率\(T(x^{t + 1}|x^{t})\),则有:
\[\begin{matrix} p\left( x^{t + 1} \right) = \sum_{x}^{}{p\left( x^{t} \right)T\left( x^{t + 1} \middle| x^{t} \right)}\ \tag{12} \\ \end{matrix}\]
当马尔科夫过程达到平衡时我们认为其样本\(x\)收敛至\(p\)分布,马尔科夫的平稳条件如下所示:
\[\begin{matrix} p\left( x^{t + 1} \right)T\left( x^{t + 1} \middle| x^{t} \right) = p\left( x^{t} \right)T\left( x^{t} \middle| x^{t + 1} \right)\ \tag{13} \\ \end{matrix}\]
在概率图模型中,对于变量概率的估计最常用的即为MCMC采样。我们根据有向图的拓扑顺序采样每一个变量,即使用马氏链进行采样,保证了算法的高效和无重复性。其中MCMC中的代表算法即为Gibbs采样,通过若干次数据的交替采样和模型参数的估计最终达到平稳过程。
变分推断
变分推断(Variational Inference, VI)是贝叶斯近似推断方法中的一大类方法,将后验推断问题巧妙地转化为优化问题进行求解,相比另一大类方法马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo, MCMC),VI 具有更好的收敛性和可扩展性(scalability),更适合求解大规模近似推断问题。
考虑一个一般性问题,\(x\)是\(n\)维的观测变量,\(z\)是\(m\)维的隐变量,贝叶斯模型中需要计算后验分布,如下:
\[\begin{matrix} p\left( z \middle| x \right) = \frac{p(z)p\left( x \middle| z \right)}{p(x)}\ \tag{14} \\ \end{matrix}\]
变分推断假设后验分布用一个变分分布\(q(z;\theta)\)来近似,通常构造如下优化问题:
\[\begin{matrix} \min_{\theta}{KL(q(z;\theta)|\left| p\left( z \middle| x;\phi \right) \right)}\ \tag{15} \\ \end{matrix}\]
可以通过求解使得两个分布距离最小的变分分布参数\(\theta\),从而得到近似后验分布。因为真实后验分布是未知的,变分推断将其转化为ELBO的问题,推导如下:
\[{KL(q(z;\theta)||p(z|x;\phi)) }{= \int_{}^{}{q(z;\theta)\log\frac{q(z;\theta)}{p\left( z \middle| x;\phi \right)}} }{= E_{q(z;\theta)}\log\frac{q(z;\theta)p(x)}{p(x,z)}\ }{= E_{q(z;\theta)}\log\frac{q(z;\theta)}{p(x,z)} + \log{p(x)} }\begin{matrix} = - ELBO(x;\theta;\phi) + \log{p(x)}\ {16} \\ \end{matrix}\]
由KL散度的定义可知,KL\(\geq\) 0,所以求优化问题(16)等价于求如下优化问题:
\[\begin{matrix} \max_{\theta}{ELBO(x;\theta,\phi)}\ \tag{17} \\ \end{matrix}\]
这里的目标函数ELBO称为Evidence Lower Bound,继续推导如下:
\[{ELBO(x;\theta,\phi) }{= E_{q(z;\theta)}\log\frac{p\left( x \middle| z;\phi \right)p(z)}{q(z;\theta)} }\begin{matrix} = E_{q(z;\theta)}\left\lbrack \log{p\left( x \middle| z;\phi \right) + \log\frac{p(z)}{q(z;\theta)}} \right\rbrack\ \tag{18} \\ \end{matrix}\]
进一步整理可得:
\[\begin{matrix} ELBO(x;\theta,\phi) = E_{q(z;\theta)}\left\lbrack \log{p\left( x \middle| z;\phi \right)} \right\rbrack - KL\left( q(z;\theta) \middle| |p(z) \right)\ \tag{19} \\ \end{matrix}\]
其中第一项可以理解为基于变分后验分布的重建似然函数,第二项是变分后验分布与先验分布的KL散度。ELBO的形式推导是VI的基础,从 ELBO 的形式可以看出,待优化的目标函数是一个函数的期望,如何高效估计出目标的梯度是解决问题的关键。
结论
概率图模型带来的一大好处是提供了⼀种简单的方式将概率模型的结构可视化,使得我们能够快速、直观的针对具体任务设计新的模型。通过观察图形,我们可以更深刻地认识模型的性质,此外⾼级模型的推断和学习过程中的复杂计算也可以根据图计算表达。有关概率图模型作为机器学习的重要组成部分,即使实在深度学习红得发紫的今天,其仍有不可撼动的地位,其学习和推理的相关知识仍有其宝贵的价值和启发意义。在其它领域,概率图模型也得到了广泛的应用。
[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.
[2] 邱锡鹏. 神经网络与深度学习[M]. 北京:机械工业出版社, 2020.04.