图论

发表于

图的搜索

深度优先搜索(DFS)

1
2
3
4
5
def dfs(root):
    if not root:
        return
    dfs(root.left)
    dfs(root.right)

广度优先搜索(BFS)

1
2
3
4
5
6
7
8
9
10
from collections import deque
def bfs(root):
    q=deque()
    q.add(root)
    while q:
        node=q.popleft()
        if node.left:
            q.append(node.left)
        if node.right:
            q.append(node.right)

图的遍历

图的遍历问题是从图中某一顶点出发，系统地访问图中所有顶点，使每个顶点恰好被访问一次。
目前，图的遍历问题分为四类：

  1. 欧拉通路与欧拉回路问题：遍历完所有的边而不能有重复，即一笔画问题
  2. 中国邮递员问题：遍历完所有的边而可以有重复
  3. 哈密尔顿问题：遍历完所有的顶点而没有重复
  4. 旅行推销员问题：遍历完所有的顶点而可以重复

目前，欧拉回路问题与中国邮递员问题已有了完美的解决方法，而哈密尔顿问题与旅行推销员问题只得到了部分解决。

欧拉通路-欧拉回路

  • 欧拉通路： 通过图中的每条边且只通过一次，并且经过每一顶点的通路。图连通，图中只有0个或者2个度为奇数的节点。
  • 欧拉回路：通过途中每条边且只通过一次，并且经过每一个顶点的回路。图连通，图中所有节点度均为偶数。

具有欧拉回路的无向图为欧拉图。具有欧拉通路但不具有欧拉回路的无向图为半欧拉图。

方法一———回溯

用DFS 搜索思想求解欧拉回路的思路为：利用欧拉定理判断出一个图存在欧拉通路或回路后，选择一个正确的起始顶点，用DFS 算法遍历所有的边（每条边只遍历一次），遇到走不通就回退。在搜索前进方向上将遍历过的边按顺序记录下来。这组边的排列就组成了一条欧拉通路或回路。

方法二——Fleury算法

设G为一无向欧拉图，求G中一条欧拉回路的算法为：
1）任取G中一顶点\(v_0\),另\(P_0=v_0\);
2) 假设\(P_i=v_0e_1...e_iv_i\)走到\(v_i\)，按下面方法从\(E(G)-\left\{ e_1,e_2,...,e_i\right\}\)中选\(e_{i+1}\)
  a) \(e_{i+1}\)与\(v_i\)相关联
  b) 除非无别的边可供选择，否则\(e_{i+1}\)不应该是\(G_i\)中的割边
3) 当2)不能再进行时算法停止 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def Fleury(g,e):    #g:图    e:起始顶点
    e1 = e
    p = []
    p.append(e)

    node_num=g.number_of_nodes()
    for i in range(1, node_num):
        if g.degree(i) % 2 != 0:
            print("不为欧拉图")
            return p
    #判断是否是欧拉图
    while 1:
        t = []
        for i in g.neighbors(e1):
            t.append(i)
        #用t接收所有邻接节点
        if len(t) == 1:
            g.remove_edge(e1, t[0])
            g.remove_node(e1)
            e1 = t[0]
            p.append(e1)
        #是悬挂节点直接选取，然后删去节点以及边
        else:
            for j in t:
                g.remove_edge(e1, j)
                if nx.is_connected(g):
                    e1 = j
                    p.append(e1)
                    break
                else:
                    g.add_edge(e1, j)
            #判断删去边后图是否连通，如果连通就直接加入路径，如不连通将删去的边接回去，继续判断下一个节点
        if e1 == e and g.size()==0:
            break
        #找到回路并且所有边都遍历一遍过后，结束循环
    return p

哈密顿问题

概念

  1. 哈密尔顿通路：经过图中每个结点且仅经过一次的通路。
  2. 哈密尔顿回路：经过图中每个结点且仅经过一次的回路。
  3. 哈密尔顿图：存在哈密尔顿回路的图。
  4. 竞赛图：每对顶点之间都有一条边相连的有向图，n 个顶点的竞赛图称为 n 阶竞赛图。
  5. 与欧拉回路的对比：欧拉回路是指不重复地走过所有路径的回路；哈密尔顿回路是指不重复地走过所有点并且最后回到起点的回路。

判定

  1. 哈密尔顿通路的判定
    设一个无向图有n个顶点，u、v为图中任意不相邻的两点，deg(x)代表x的度数。若deg(u)+deg(v)\(\geqslant\)n-1成立，则图中存在哈密尔顿通路
  2. 哈密尔顿回路的判定：Dirac定理
    deg(u)+deg(v)\(\geqslant\)n成立，则图中存在哈密尔顿回路
    推论：对于n\(\geqslant\) 3的无向图，若任一点的度数deg(u)\(\geqslant\) n/2，则图中存在哈密尔顿回路
  3. 竞赛图
    对于n \(\geqslant\) 2的竞赛图，一定存在哈密尔顿回路

AOV(Activity On Vertex)网与拓扑排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def topoSort(graph):     
    in_degrees = dict((u,0) for u in graph)   #初始化所有顶点入度为0     
    num = len(in_degrees)     
    for u in graph:         
        for v in graph[u]:             
            in_degrees[v] += 1    #计算每个顶点的入度     
    Q = [u for u in in_degrees if in_degrees[u] == 0]   # 筛选入度为0的顶点     
    Seq = []     
    while Q:         
        u = Q.pop()       #默认从最后一个删除         
        Seq.append(u)         
        for v in graph[u]:             
            in_degrees[v] -= 1    #移除其所有出边
            if in_degrees[v] == 0:        
                Q.append(v)          #再次筛选入度为0的顶点
    if len(Seq) == num:       #输出的顶点数是否与图中的顶点数相等
        return Seq     
    else:         
        return None

G = {
    'a':'bf',
    'b':'cdf',
    'c':'d',
    'd':'ef',
    'e':'f',
    'f':''
}
print(topoSort(G))

AOE网与关键路径

概念

在表示一个工程时，用顶点表示事件，用弧表示活动，权值表示活动的持续时间，这样的有向图即为AOE网，其有两个性质： + 在顶点表示事件发生之后，从该顶点出发的有向弧所表示的活动才能开始。 + 在进入某个顶点的有向弧所表示的活动完成之后，该顶点表示的事件才能发生。

在 AOE 网中，只有一个入度为 0 的点表示工程的开始，即源点，也只有一个出度为 0 的点表示工程的结束，即汇点。

关键路径

关键路径是指在AOE网中从源点到汇点路径最长的路径。这里的路径长度是指路径上各个活动持续时间之和。在AOE网中，有些活动是可以并行执行的，关键路径其实就是完成工程的最短时间所经过的路径。关键路径上的活动称为关键活动。
1. 事件\(v_i\)的最早发生时间：从源点到顶点\(v_i\)的最长路径长度，称为事件\(v_i\)的最早发生时间，记作ve(i)。求解ve(i)可以从源点ve(0)=0开始，按照拓扑排序的规则递推得到： \[ve(i)=MAX\lbrace ve(k)+dut(<k,j>)|<k,j>\in T,1\leq i\leq n-1\rbrace\] 2. 事件\(v_i\)的最晚发生时间：在保证整个工程完成的前提下，活动最迟的开始时间，记作\(vl(i)\)。在求解\(v_i\)的最早发生时间的前提下，从汇点开始，向源点推进得到： \[vl(i)=MIN\lbrace vl(k)-dut(<i,k>)|<i,k>\in T,0\leq i\leq n-2\rbrace\] 3. 松弛时间：活动\(a_i\)的最晚开始时间与最早开始时间之差就是活动\(a_i\)的松弛时间。

伪代码流程

1
2
3
4
1. 对AOE网中的顶点进行拓扑排序，如果得到的拓扑序列顶点个数小于网中顶点数，则说明网中有环存在，不能求关键路径，终止算法。否则，从源点v0开始，求出各个顶点的最早发生时间ve(i)。
  2. 从汇点vn出发vl(n-1)=ve(n-1)，按照逆拓扑序列求其他顶点的最晚发生时间vl(i)。
  3. 由各顶点的最早发生时间ve(i)和最晚发生时间vl(i)，求出每个活动ai的最早开始时间e(i)和最晚开始时间l(i)。
  4. 找出所有满足条件e(i)=l(i)的活动ai，ai即是关键活动。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
node_list = ['A','B','C','D','E','F','G','H','I']
edge_list = [['A','B',  6],
                ['A', 'C', 4],
                ['A', 'D', 5],
                ['B', 'E', 1],
                ['C', 'E', 1],
                ['D', 'H', 2],
                ['E', 'F', 9],
                ['E', 'G', 7],
                ['F', 'I', 2],
                ['G', 'I', 4],
                ['H', 'I', 4],
                ]

def find_shorted_path():
    global node_list,edge_list
    
    '''计算各个顶点的Ve(v)最早发生时间'''

    #找出图的起点
    temp_start_list = []
    for edge in edge_list:
        temp_start_list.append(edge[1])
    start_node = [x for x in node_list if x not in temp_start_list]
    # print(start_node)

    Ve_node_dict = {}
    Ve_node_dict[start_node[0]] = 0

    for node in node_list:
        Ve_tempnode_list = []
        for edge in edge_list:
            if node == edge[1]:
                temp_Ve_node_value = Ve_node_dict[edge[0]] + edge[2]
                Ve_tempnode_list.append(temp_Ve_node_value)
        if len(Ve_tempnode_list) == 0:
            Ve_node_dict[node] = 0
        if len(Ve_tempnode_list) == 1:
            Ve_node_value = Ve_tempnode_list[0]
            Ve_node_dict[node] = Ve_node_value
        if len(Ve_tempnode_list) > 1:
            Ve_node_value = max(Ve_tempnode_list)
            Ve_node_dict[node] = Ve_node_value
    print('Ve(v)最早发生时间:\n',Ve_node_dict,'\n')

    '''计算各个顶点的Vl(v)最迟发生时间'''

    #找出图的终点
    temp_end_list = []
    for edge in edge_list:
        temp_end_list.append(edge[0])
    end_node = [x for x in node_list if x not in temp_end_list]
    # print(end_node)

    Vl_node_dict = {}
    Vl_node_dict[end_node[0]] = Ve_node_dict[end_node[0]]

    reverse_edge_list = []
    for i in range(len(edge_list)-1,-1,-1):
        reverse_edge_list.append(edge_list[i])


    for node in reversed(node_list):
        Vl_tempnode_list = []
        for edge in reverse_edge_list:
            if node == edge[0]:
                temp_Vl_node_value = Vl_node_dict[edge[1]] - edge[2]
                Vl_tempnode_list.append(temp_Vl_node_value)
        if len(Vl_tempnode_list) == 0:
            Vl_node_dict[node] = Ve_node_dict[end_node[0]]
        if len(Vl_tempnode_list) == 1:
            Vl_node_value = Vl_tempnode_list[0]
            Vl_node_dict[node] = Vl_node_value
        if len(Vl_tempnode_list) > 1:
            Vl_node_value = min(Vl_tempnode_list)
            Vl_node_dict[node] = Vl_node_value
    print('Vl(v)最迟发生时间:\n',Vl_node_dict,'\n')

    '''计算各个边的e(a)最早发生时间'''

    e_bian_dict = {}
    for edge in edge_list:
        e_bian_dict['{}-{}'.format(edge[0],edge[1])] = Ve_node_dict[edge[0]]
    print('e(a)最早发生时间:\n',e_bian_dict,'\n')

    '''计算各个边的l(a)最迟发生时间'''

    l_bian_dict = {}
    for edge in edge_list:
        l_bian_dict['{}-{}'.format(edge[0],edge[1])] = Vl_node_dict[edge[1]] - edge[2]
    print('l(a)最迟发生时间:\n',l_bian_dict,'\n')

    '''计算时间余量d(a)'''

    d_bian_dict = {}
    for bian in e_bian_dict.keys():
        d_bian_dict[bian] = l_bian_dict[bian] - e_bian_dict[bian]
    print("d(a)时间余量:\n",d_bian_dict,'\n')

    print("关键路径为：",[x for x in d_bian_dict if d_bian_dict[x] == 0])

if __name__ == "__main__":
    find_shorted_path()

图的连通性

连通图与联通分量

1）连通图：无向图 G 中，若对任意两点，从顶点 Vi 到顶点 Vj 有路径，则称 Vi 和 Vj 是连通的，图 G 是一连通图

2）连通分量：无向图 G 的连通子图称为 G 的连通分量

任何连通图的连通分量只有一个，即其自身，而非连通的无向图有多个连通分量

强连通图和强联通分量

1）强连通图：有向图 G 中，若对任意两点，从顶点 Vi 到顶点 Vj，都存在从 Vi 到 Vj 以及从 Vj 到 Vi 的路径，则称 G 是强连通图

2）强连通分量：有向图 G 的强连通子图称为 G 的强连通分量

强连通图只有一个强连通分量，即其自身，非强连通的有向图有多个强连通分量。

最短路径算法

Floyd算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
def getPath(i, j):
    if i != j:
        if path[i][j] == -1:
            print('-', j+1, end='')
        else:
            getPath(i, path[i][j])
            getPath(path[i][j], j)

def printPath(i, j):
    print(' Path:', i+1, end='')
    getPath(i, j)
    print()
'''
flag(1:directed,2:undirected)
vertex 
edge
inf=float('inf')
dis :matrix of the shortest distance
path :record the shortest path
'''
# floyd algorithm
def floyd():
    nonlocal vertex,dis,path
    for k in range(vertex):
        for i in range(vertex):
            for j in range(vertex):
                if dis[i][j] > dis[i][k] + dis[k][j]:
                    dis[i][j] = dis[i][k] + dis[k][j]
                    path[i][j] = k

# output the result
if flag == 1:
    for i in range(vertex):
        for j in range(vertex):
            if (i != j) and (dis[i][j] != inf):
                print('v%d ----> v%d  tol_weight:'
                      '%3d' % (i+1, j+1, dis[i][j]))
                printPath(i, j)
            if (i != j) and (dis[i][j] == inf):
                print('v%d ----> v%d  tol_weight:'
                      '  ∞' % (i+1, j+1))
                printPath(i, j)

if flag == 2:
    for i in range(vertex):
        for j in range(i+1, vertex):
            print('v%d <----> v%d  tol_weight:'
                  '%3d' % (i+1, j+1, dis[i][j]), '', end='')
            printPath(i, j)

for i in range(vertex):
    for j in range(vertex):
        if dis[i][j] == inf:
            dis[i][j] = 0

Dijkstra 算法

概述

Dijkstra 算法是单源最短路径算法，即计算起点只有一个的情况到其他点的最短路径，其无法处理存在负边权的情况。其时间复杂度是：O(E+VlogV)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import networkx as nx

def Dijkstra(G,start,end):
    RG = G.reverse()
    dist = {} 
    previous = {}
    for v in RG.nodes():
        dist[v] = float('inf')
        previous[v] = 'none'
    dist[end] = 0
    u = end
    while u!=start:
        u = min(dist, key=dist.get)
        distu = dist[u]
        del dist[u]
        for u,v in RG.edges(u):
            if v in dist:
                alt = distu + RG[u][v]['weight']
                if alt < dist[v]:
                    dist[v] = alt
                    previous[v] = u
    path=(start,)
    last= start
    while last != end:
        nxt = previous[last]
        path += (nxt,)
        last = nxt
    return path

Bellman-Ford 算法

概述

Bellman-Ford算法适用于计算单源最短路径，即：只能计算起点只有一个的情况。 其最大特点是可以处理存在负边权的情况，但无法处理存在负权回路的情况。 其时间复杂度为：O(V*E)，其中，V 是顶点数，E 是边数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def bellman_ford(graph, source):
    dist = {}
    p = {}
    max = 10000
    for v in graph:
        dist[v] = max  #赋值为负无穷完成初始化
        p[v] = None
    dist[source] = 0
 
    for i in range(len( graph ) - 1):
        for u in graph:
            for v in graph[u]:
                if dist[v] > graph[u][v] + dist[u]:
                    dist[v] = graph[u][v] + dist[u]
                    p[v] = u    #完成松弛操作，p为前驱节点
 
    for u in graph:
        for v in graph[u]:
            if dist[v] > dist[u] + graph[u][v]:
                return None, None  #判断是否存在环路
 
    return dist, p
 
graph = {
    'a': {'b': -1, 'c':  4},
    'b': {'c':  2, 'd':  3, 'e':  2},
    'c': {},
    'd': {'b':  3, 'c':  5},
    'e': {'d': -3}
}
dist, p = bellman_ford(graph, 'a')

差分约束系统与最短路径

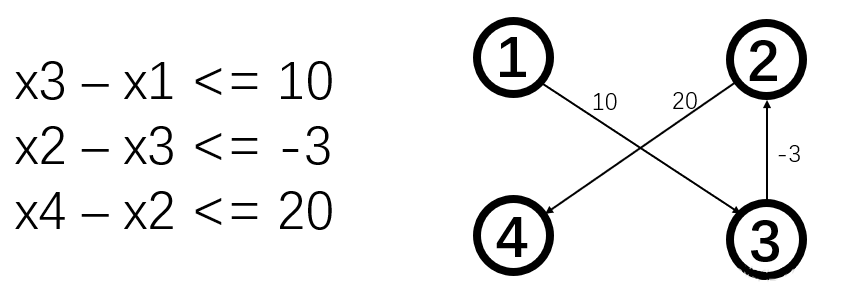
何为差分约束系统

如果一个系统由n个变量和m个约束条件组成，约束条件形如 xi - xj <= k(i,j∈[1,n])，则成为差分约束系统。
例如：
x1-x3 <= 5
x1-x2 <= 2
x2-x3 <= 1

差分约束系统的求解

以上式差分约束系统为例，若想求x1到x3的最小值，我们可以由第一个约束条件看出x1 - x3的最大值是5，但通过把第二个与第三个不等式相加，我们可以得到：x1 - x3 <= 3，最后我们验证3才是最优解。现在我们把约束条件xi - xj <= k移项，可得：xi <= xj + k，并设x1 = 0再模拟上述过程，我们发现，当且仅当xi <= xj + k时，xi的值被改变成了xj + k，学习过最短路径的hxd相信已经发现了其中的奥秘。在SPFA，dijkstra等最短路算法中，当xi <= xj + k时，我们进行两点之间的松弛操作，即更新源点到点xi的最短路径为xj + k。

差分约束系统与最短路径

差分约束系统的解法用到了单源最短路径问题中的三角形不等式。对有向图中的一条边<u,v>来说，都有dis[v]≤dis[u]+len[u][v]，其中dis[u]表示源点到u结点的最短路径，v结点同理。len[u][v]表示，u与v的边的长度。三角不等式是显然的，从源点到顶点v的最短路径长度小于等于从源点到顶点 u的最短路径长度加上边 <u,v> 的长度值。

与有向图结合的例子

A*算法

伪代码流程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
创建开启列表、关闭列表
将起始点加入开放列表中
弹出开启列表的第一个节点，将该元素作为当前节点
while(当前节点不为终点时)：	
	获取并处理当前节点的周围可通过的节点，
		为这些节点设置G值、H值，
		添加当前节点为这些可通过节点的父节点
	遍历当前节点的周围节点
		if(该节点可通过且不在关闭列表):
			if(该节点在开启列表):
				根据 估价函数F(n)进行比较
				if(开启列表的节点的估价函数大于该节点的估价函数):
					将开启列表的节点进行覆盖
			else:
				将该节点加入开启列表
	将当前节点添加到关闭列表中
	对开启列表进行排序
	当前节点<-获得开启列表的第一个元素
创建一个路径结果集
while(当前节点的父节点不为空):
	获得当前节点的索引，存入路径结果集中
	当前节点<-当前节点的父节点
返回路径结果集
结束

地图对象

1
2
3
4
5
6
7
8
import math
class Map(object):
    def __init__(self,mapdata,startx,starty,endx,endy):
        self.data = mapdata
        self.startx = startx
        self.starty = starty
        self.endx = endx
        self.endy = endy

结点对象

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
# Manhattan Distance
class Node(object):
    def __init__(self,x,y,g,h,father):
        self.x = x
        self.y = y
        self.g = g
        self.h = h
        self.father = father
    def getNeighbor(self,mapdata,endx,endy):
        x = self.x
        y = self.y
        result = []
        if(x!=0 and mapdata[x-1][y]!=0):
            upNode = Node(x-1,y,self.g+10,(abs(x-1-endx)+abs(y-endy))*10,self)
            result.append(upNode)
    #dwon
        if(x!=len(mapdata)-1 and mapdata[x+1][y]!=0):
            downNode = Node(x+1,y,self.g+10,(abs(x+1-endx)+abs(y-endy))*10,self)
            result.append(downNode)
    #left
        if(y!=0 and mapdata[x][y-1]!=0):
            leftNode = Node(x,y-1,self.g+10,(abs(x-endx)+abs(y-1-endy))*10,self)
            result.append(leftNode)
    #right
        if(y!=len(mapdata[0])-1 and mapdata[x][y+1]!=0):
            rightNode = Node(x,y+1,self.g+10,(abs(x-endx)+abs(y+1-endy))*10,self)
            result.append(rightNode)
    #west-notrh  dist=14
        if(x!=0 and y!=0 and mapdata[x-1][y-1]!=0 ):
            wnNode = Node(x-1,y-1,self.g+14,(abs(x-1-endx)+abs(y-1-endy))*10,self)
            result.append(wnNode)
    #east-north
        if(x!=0 and y!=len(mapdata[0])-1 and mapdata[x-1][y+1]!=0 ):
            enNode = Node(x-1,y+1,self.g+14,(abs(x-1-endx)+abs(y+1-endy))*10,self)
            result.append(enNode)
    #west-south
        if(x!=len(mapdata)-1 and y!=0 and mapdata[x+1][y-1]!=0 ):
            wsNode = Node(x+1,y-1,self.g+14,(abs(x+1-endx)+abs(y-1-endy))*10,self)
            result.append(wsNode)
    #east-south
        if(x!=len(mapdata)-1 and y!=len(mapdata[0])-1 and mapdata[x+1][y+1]!=0 ):
            esNode = Node(x+1,y+1,self.g+14,(abs(x+1-endx)+abs(y+1-endy))*10,self)
            result.append(esNode)
        return result

    def hasNode(self,worklist):
        for i in worklist:
            if(i.x==self.x and i.y ==self.y):
                return True
        return False
    #在存在的前提下 hasNode=True
    def changeG(self,worklist):
        for i in worklist:
            if(i.x==self.x and i.y ==self.y):
                if(i.g>self.g):
                    i.g = self.g

A*路径算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from Node import Node
def getKeyforSort(element:Node):
    return element.g #element#不应该+element.h，否则会穿墙
def astar(workMap):
    startx,starty = workMap.startx,workMap.starty
    endx,endy = workMap.endx,workMap.endy
    startNode = Node(startx, starty, 0, 0, None)
    openList = []
    lockList = []
    lockList.append(startNode)
    currNode = startNode
    while((endx,endy) != (currNode.x,currNode.y)):
        workList = currNode.getNeighbor(workMap.data,endx,endy)
        for i in workList:
            if (i not in lockList):
                if(i.hasNode(openList)):
                    i.changeG(openList)
                else:
                    openList.append(i)
        openList.sort(key=getKeyforSort)#关键步骤
        currNode = openList.pop(0)
        lockList.append(currNode)
    result = []
    while(currNode.father!=None):
        result.append((currNode.x,currNode.y))
        currNode = currNode.father
    result.append((currNode.x,currNode.y))
    return result

主函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from astar import astar
from Map import Map
mymap = [
    [1,1,1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1],
    [1,1,1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],
    [1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1],
    [1,1,1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1],
    [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1],
    [1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1],
    [1,1,1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1],
    [1,1,1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1],
    [1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1]
    ]
map = Map(mymap,0,1,5,5)
result = astar(map)
result.reverse()
print(result)

最小生成树

概述

最小生成树的定义：最小生成树是一副连通加权无向图中一棵权值最小的生成树。
在一给定的无向图G=(V,E)中，(u,v)代表连接顶点u与顶点v的边,而w(u,,v)代表此边的权重，若存在T为E的子集且(V,T)为树，使得 \[w(T)=\sum_{(u,v)\in T}w(u,v)\] 的w(T)最小，则称此T为G的最小生成树

Prim算法

1.用两个集合A{}，B{}分别表示找到的点集，和未找到的点集
2.我们以A中的点为起点a，在B中找一个点为终点b，这两个点构成的边（a，b）的权值是其余边中最小的
3.重复上述步骤#2，直至B中的点集为空，A中的点集为满

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import sys
def prim(graph,n):
    '''
    prim算法求最小生成树
    :param graph: 图
    :return: 最小的权值
    :n:点的个数
    '''
    lowcost = [] #记录当前顶点集合到剩下的点的最低权值，“-1”表示已访问过的点，无需访问
    mst = [] #记录当前被更新的最低权值来自于哪个点，相当于记录是边的起始点，lowcost的下标表示的是最低权值的终止点
    cost = 0 #记录整个最小生成树的权值
    for i in range(n): #初始化lowcost与mst，默认先选择第0个点，把第0个点到其余所有点的权值赋给lowcost，mst内全部赋值为0（也就是第0个点为起始）
        lowcost.append(graph[0][i])
        mst.append(0)
    v = 0 #记录当前被选择的点
    lowcost[0] = -1 #用“-1"来标记被选择的点，
    for i in range(n-1):
        min = sys.maxsize #初始为最大值，作用是记录当前最低权值
        for j in range(n):
            if(min > lowcost[j] and lowcost[j] != -1):
                min = lowcost[j]
                v = j
        cost += min
        print(traver(mst[v]),"->",traver(v),": ",min)
        lowcost[v] = -1 #用”-1“标记被选择的点
        for k in range(n): #更新lowcost
            if(lowcost[k] > graph[v][k]):
                lowcost[k] = graph[v][k]
                mst[k] = v #如果有被更新的权值，就把当前点作为被更新权值的那条边的起始点

    return cost

def traver(x):
    return chr(x+97)


if __name__=='__main__':
    MAX = sys.maxsize
    graph = [[MAX,6,1,5,MAX,MAX],
             [6,MAX,5,MAX,3,MAX],
             [1,5,MAX,5,6,4],
             [5,MAX,5,MAX,MAX,2],
             [MAX,3,6,MAX,MAX,6],
             [MAX,MAX,4,2,6,MAX]]
    print(prim(graph,len(graph)))

Kruskal

Kruskal 算法基本思想是并查集思想，将所有边升序排序，并认为每一个点都是孤立的，分属 n 个独立的集合。按顺序枚举每一条边，如果这条边连接的两个点分属两个不同的集合，那么就将这条边加入最小生成树，这两个不同的集合合并为一个集合；如果这条边连接的两个点属于同一集合，那么就跳过。直到选取 n-1条边为止（只剩一个集合）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 查
def find(father, u):
    if u != father[u]:
        father[u] = find(father, father[father[u]])
    return father[u]

# 并
def union(father, R, u, v):
    u = find(father, u)
    v = find(father, v)
    if R[u] > R[v]:
        father[v] = u
    else:
        father[u] = v
    if R[u] == R[v]:
        R[v] += 1

def kruskal(G):
    E = [(G[u][v], u, v) for u in G for v in G[u]]
    T = set()
    father, R = {u:u for u in G}, {u:0 for u in G}
    for _, u, v in sorted(G):
        if find(father, u) != find(father, v):
            T.add(set(u, v))
            union(father, R, u, v)
    return T

最小瓶颈生成树

所谓瓶颈生成树，即对于图 G 中的生成树树上最大的边权值在所有生成树中最小。对于无向图来说，无向图的最小生成树一定是最小瓶颈生成树，但最小瓶颈生成树不一定是最小生成树。因此，使用 Kruskal 算法即可求出无向图的最小瓶颈生成树。

次小生成树

对于给定的无向图 G=（V,E），设 T 是图 G 的一个最小生成树，那么，对于除 T 外的第二小的生成树 T' 即为图的次小生成树。简单来说，最小生成树是生成树的最小解，次小生成树是生成树的次小解，它有可能和最小生成树的值一样，但肯定不能比最小生成树的值要小。

一般来说，求最小生成树的算法是 Prim 或 Kurskal，那么对于次小生成树，同样可以使用这两种算法来解。对于求次小生成树来说，两种算法的思路都是相同的。首先求出最小生成树，再枚举每条不在最小生成树上的边，并把这条边放到最小生成树上面，此时一定会形成环，那么在这条环路中取出一条除新加入的边外的最长路，最终得到的权值就是次小生成树的权值。

最小树形图

最小树形图，就是给出一个带权有向图，从中指定一个特殊的结点 root，求一棵以 root 为根的有向生成树 T，且使得 T 中所有边权值最小。简单来说，最小树形图就是有向图的最小生成树。

算法概述

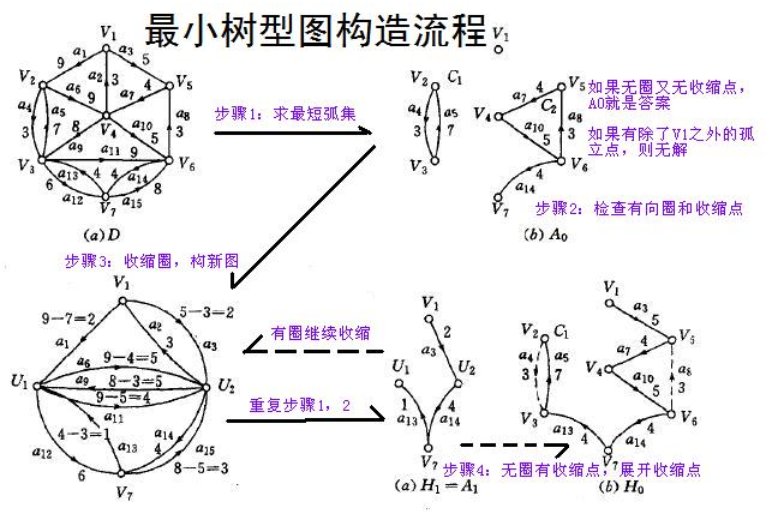
为了求一个图的最小树形图，①先求出最短弧集合E0；②如果E0不存在，则图的最小树形图也不存在；③如果E0存在且不具有环，则E0就是最小树形图；④如果E0存在但是存在有向环，则把这个环收缩成一个点u，形成新的图G1，然后对G1继续求其的最小树形图，直到求到图Gi，如果Gi不具有最小树形图，那么此图不存在最小树形图，如果Gi存在最小树形图，那么逐层展开，就得到了原图的最小树形图。

实现细节

设根结点为v0

（1）求最短弧集合E0
　　从所有以vi(i ≠ 0)为终点的弧中取一条最短的，若对于点i，没有入边，则不存在最小树形图，算法结束；如果能取，则得到由n个点和n-1条边组成的图G的一个子图G'，这个子图的权值一定是最小的，但是不一定是一棵树。

（2）检查E0
　　若E0没有有向环且不包含收缩点,则计算结束，E0就是图G以v0为根的最小树形图；若E0含有有向环，则转入步骤(3)；若E0没有有向环,但是存在收缩点，转到步骤(4)。

（3）收缩G中的有向环
　　把G中的环C收缩成点u，对于图G中两端都属于C的边就会被收缩掉，其他弧仍然保留，得到一个新的图\(G_1\)，\(G_1\)中以收缩点为终点的弧的长度要变化。变化的规则是：设点v在环C中，且环中指向v的边的权值为w，点v'不在环C中，则对于G中的每一条边<v', v>，在G1中有边<v', u>和其对应，且权值\(W_{G1}\)(<v', u>) = \(W_{G}\)(<v', v>) - w；对于图G中以环C中的点为起点的边<v', v>，在图\(G_1\)中有边<u, v'>，则\(W_{G1}\)(<u, v'>) = \(W_{G}\)(<v', v>)。有一点需要注意,在这里生成的图\(G_1\)可能存在重边。

　　对于图G和\(G_1\)：

　　①如果图\(G_1\)中没有以v0为根的最小树形图，则图G也没有；

　　②如果\(G_1\)中有一v0为根的最小树形图，则可按照步骤（4）的展开方法得到图G的最小树形图。

所以，应该对于图G1代到(1)中反复求其最小树形图，直到G1的最小树形图u求出。

（4）展开收缩点
　　假设图G1的最小树形图为T1,那么T1中所有的弧都属于图G的最小树形图T。将G1的一个收缩点u展开成环C，从C中去掉与T1具有相同终点的弧，其他弧都属于T。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
class Edge:
    def __init__(self, u, v, w):
        self.u = u
        self.v = v
        self.w = w

    def __str__(self):
        return str(self.u) + str(self.v) + str(self.w)


def zhuliu(edges, n, m, root):
    res = 0
    while True:
        pre = [-1]*n
        visited = [-1] * n
        circle = []
        inderee = [INF] * n
        # 寻找最小入边
        inderee[root] = 0
        for i in range(m):
            if edges[i].u != edges[i].v and edges[i].w < inderee[edges[i].v]:
                pre[edges[i].v] = edges[i].u
                inderee[edges[i].v] = edges[i].w
        # 有孤立点，不存在最小树形图
        for i in range(n):
            if i != root and inderee[i] == INF:
                return -1
        # 找有向h环
        tn = 0  # 记录环的个数
        circle = [-1] * n
        for i in range(n):
            res += inderee[i]
            v = i
            # 向前遍历找环，中止情况有：
            # 1. 出现带有相同标记的点，成环
            # 2. 节点属于其他环，说明进了其他环
            # 3. 遍历到root了
            while visited[v] != i and circle[v] == -1 and v != root:
                visited[v] = i
                v = pre[v]
            # 如果成环了才会进下面的循环，把环内的点的circle进行标记
            if v != root and circle[v] == -1:
                while circle[v] != tn:
                    circle[v] = tn
                    v = pre[v]
                tn += 1
        # 如果没有环了，说明一定已经找到了
        if tn == 0:
            break
        # 否则把孤立点都看作自环看待
        for i in range(n):
            if circle[i] == -1:
                circle[i] = tn
                tn += 1
        # 进行缩点，把点号用环号替代
        for i in range(m):
            v = edges[i].v
            edges[i].u = circle[edges[i].u]
            edges[i].v = circle[edges[i].v]
            # 如果边不属于同一个环
            if edges[i].u != edges[i].v:
                edges[i].w -= inderee[v]
        n = tn
        root = circle[root]
    return res


INF = 9999999999
if __name__ == '__main__':
    n, m, root = list(map(int, input().split()))
    edges = []
    for i in range(m):
        u, v, w = list(map(int, input().split()))
        # 输入的点是1开始的，-1改为0开始的
        edges.append(Edge(u-1, v-1, w))
    print(zhuliu(edges, n, m, root-1),end = "")

写到这里发现了一个写的贼好的网站，大家看这个吧 图论详细介绍